
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Несинусоидальные периодические токи и принцип суперпозиции в линейных электрических цепях.
|
|
Известно, что любая несинусоидальная периодическая функция может быть разложена в ряд Фурье с коэффициентами, показывающими вклад токов (напряжений) с частотами, кратными основной, которые называются гармониками.
В общем виде
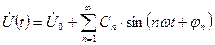 (28).
(28).
Если приведённое напряжение воздействует на участок цепи с сопротивлением 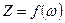 , то каждое из слагаемых в сумме (28) породит компоненту тока с частотой «
, то каждое из слагаемых в сумме (28) породит компоненту тока с частотой «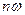 », а принцип суперпозиции позволит найти общий ток в цепи как сумму частичных токов:
», а принцип суперпозиции позволит найти общий ток в цепи как сумму частичных токов:
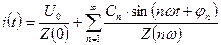 (29).
(29).
Если известны действующие значения напряжений каждой из гармоник 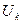 , то результирующее действующее значение напряжения
, то результирующее действующее значение напряжения 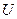 определяется выражением:
определяется выражением:
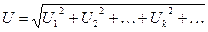 (30).
(30).
Аналогично находится действующее значение несинусоидального тока.
Всё сказанное относится только к линейным цепям.