
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Означення функції та її властивості
|
|
Означення функції. Правило (закон) відповідності між множинами  і
і  , за яким для кожного елемента
, за яким для кожного елемента  з множини
з множини  можна знайти один і тільки один елемент
можна знайти один і тільки один елемент  з множини
з множини  , називається функцією.
, називається функцією.
При цьому  називається незалежною змінною, або аргументом, а
називається незалежною змінною, або аргументом, а  –залежною змінною, або функцією. Позначення:
–залежною змінною, або функцією. Позначення:  . Множина
. Множина  всіх допустимих значень аргументу
всіх допустимих значень аргументу  , при яких функція
, при яких функція  визначена, називається областю визначення функції. Множина
визначена, називається областю визначення функції. Множина  всіх значень
всіх значень  , яких набуває функція, називається областю значень функції.
, яких набуває функція, називається областю значень функції.
Приклад 4.1. Знайти область визначення і область значень функцій:
 – область визначення функції
– область визначення функції  , область значень функції
, область значень функції 
 – область визначення функції
– область визначення функції  область значень функції
область значень функції 
 – область визначення функції
– область визначення функції  , область значень функції
, область значень функції 
Щоб задати функцію, необхідно вказати її область визначення та правило, за яким кожному значенню  з області визначення відповідає значення
з області визначення відповідає значення  . Розрізняють такі способи задання функції:
. Розрізняють такі способи задання функції:
1. Табличний спосіб, який полягає в тому, що функцію можна задати за допомогою таблиці (табл. 4.1), в якій в одному рядку (або стовпчику) записано всі значення аргументу, а в другому – відповідні значення функції.
Таблиця 4.1

| 
| 
| … | 
|

| 
| 
| … | 
|
Табличний спосіб виявляється зручним, коли область визначення функції складається із скінченного числа точок. Але при розгляді теоретичних питань, вивченні якісної поведінки функції не можна обмежуватись функціями, які визначені лише в скінченному числі точок.
2. Графічний спосіб, який полягає в тому, що подається графік цієї функції. Графік дає просте і наочне уявлення про якісну поведінку функції, але точність обчислення значень функції за допомогою графіка досить низька внаслідок похибок при проведенні перпендикулярів і вимірюванні довжин.
3. Аналітичний спосіб, який полягає в тому, що  виражають через
виражають через  за допомогою формули, що показує, які дії треба виконати з аргументом
за допомогою формули, що показує, які дії треба виконати з аргументом  , щоб отримати значення
, щоб отримати значення  . Аналітичний спосіб дає можливість обчислити значення функції при довільному значенні аргументу, при якому вона визначена точно або з довільною точністю.
. Аналітичний спосіб дає можливість обчислити значення функції при довільному значенні аргументу, при якому вона визначена точно або з довільною точністю.
4. Словесне задання функції, яке полягає в тому, що закон, за яким обчислюється  виражається словами.
виражається словами.
Нулі функції. Значення аргументу, при якому функція дорівнює  , називається нулем функції. Функція може мати декілька нулів. Наприклад, функція
, називається нулем функції. Функція може мати декілька нулів. Наприклад, функція  має три нулі:
має три нулі:  Геометрично нуль функції – це абсциса точки перетину графіка функції з віссю
Геометрично нуль функції – це абсциса точки перетину графіка функції з віссю  . На рис. 4.1 зображено графік функції з нулями
. На рис. 4.1 зображено графік функції з нулями  і
і 
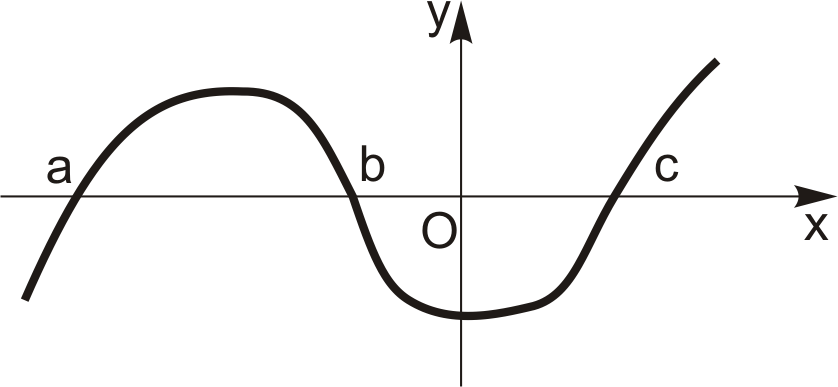
Рис. 4.1
Монотонна функція. Функція  зростає на деякому проміжку, якщо для всіх
зростає на деякому проміжку, якщо для всіх  і
і  з цього проміжку з нерівності
з цього проміжку з нерівності  випливає нерівність
випливає нерівність  . Функція
. Функція  спадає на деякому проміжку, якщо для всіх
спадає на деякому проміжку, якщо для всіх  і
і  з цього проміжку з нерівності
з цього проміжку з нерівності  випливає нерівність
випливає нерівність  . Функція, яка спадає або зростає на певному проміжку, називається монотонною на цьому проміжку.
. Функція, яка спадає або зростає на певному проміжку, називається монотонною на цьому проміжку.
Обмежена і необмежена функції. Функція називається обмеженою, якщо існує таке додатне число  , що
, що  для всіх значень
для всіх значень  . Якщо такого числа не існує, то функція не обмежена. Так, наприклад, функція на рис. 4.2 обмежена, але не монотонна, а на рис. 4.3 - монотонна, але не обмежена.
. Якщо такого числа не існує, то функція не обмежена. Так, наприклад, функція на рис. 4.2 обмежена, але не монотонна, а на рис. 4.3 - монотонна, але не обмежена.
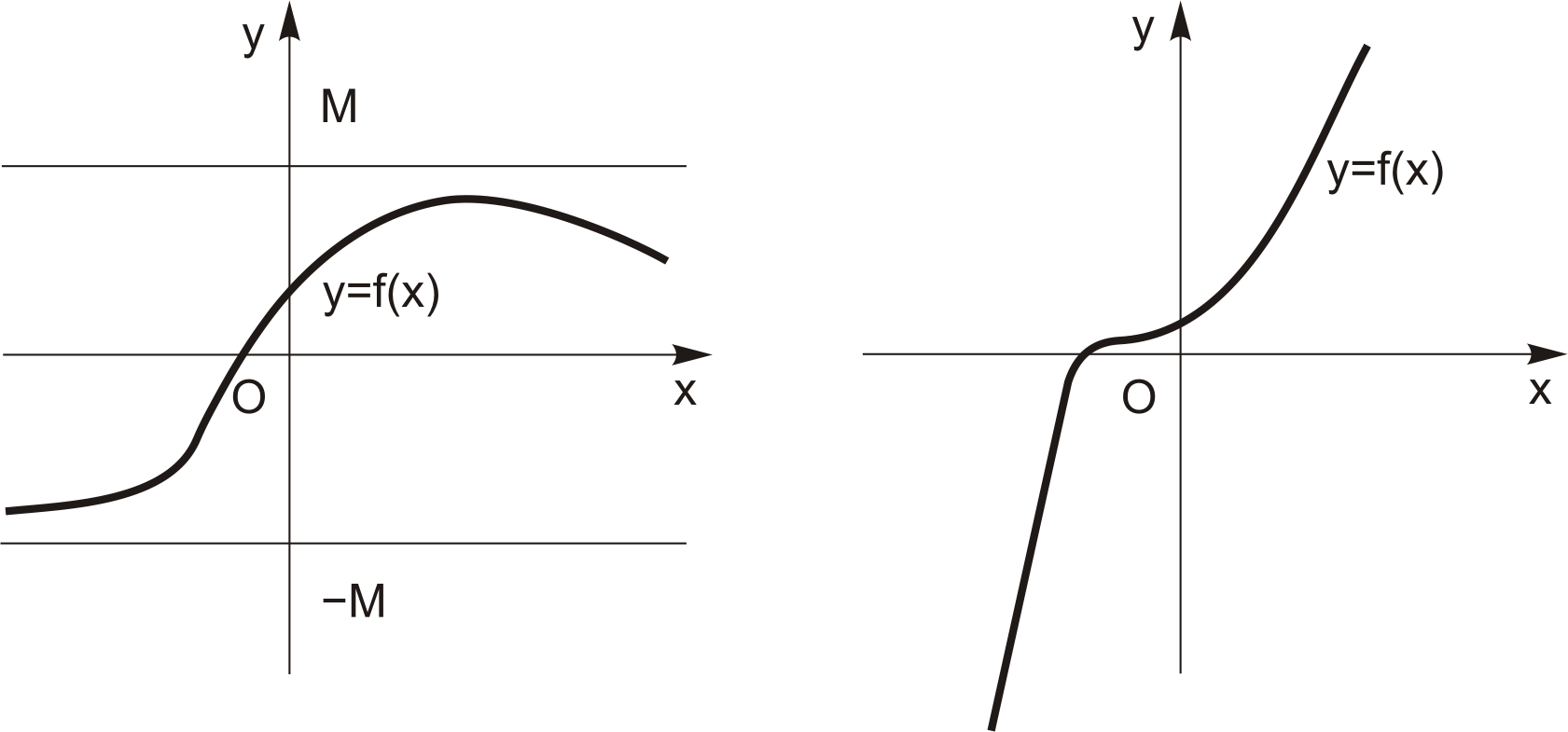
Рис. 4.2 Рис. 4. 3
Неперервна і розривна функції. Функція  називається неперервною в точці
називається неперервною в точці  , якщо:
, якщо:
1) функція визначена при  , тобто
, тобто  існує;
існує;
2) існує скінченна границя  ; 3)
; 3)  .
.
Якщо не виконується хоч одна з цих умов, то функція називається розривною в точці  . Якщо функція неперервна в кожній точці області визначення, то вона називається неперервною функцією. Функція
. Якщо функція неперервна в кожній точці області визначення, то вона називається неперервною функцією. Функція  , графік якої наведено на
, графік якої наведено на
рис. 4.4, розривна при  , оскільки не визначена при
, оскільки не визначена при  . В усіх інших точках вона неперервна. Функція
. В усіх інших точках вона неперервна. Функція  (рис. 4.5) розривна при
(рис. 4.5) розривна при  .
.
Асимптота. Якщо графік функції необмежено наближається до деякої прямої при віддаленні від початку координат, то ця пряма називається асимптотою.
Парна і непарна функції. Якщо для будь-якого  з області визначення функції виконується
з області визначення функції виконується  , то функція називається парною; якщо –
, то функція називається парною; якщо –  , то функція називається непарною. Графік парної функції симетричний відносно осі
, то функція називається непарною. Графік парної функції симетричний відносно осі  (рис. 4.6), а графік непарної функції симетричний відносно початку координат
(рис. 4.6), а графік непарної функції симетричний відносно початку координат
(рис. 4.7).
Періодична функція. Функція  – періодична, якщо існує таке відмінне від нуля число
– періодична, якщо існує таке відмінне від нуля число  , що для будь-якого
, що для будь-якого  з області визначення функції виконується рівність
з області визначення функції виконується рівність
 . Таке найменше число називається періодом функції.
. Таке найменше число називається періодом функції.
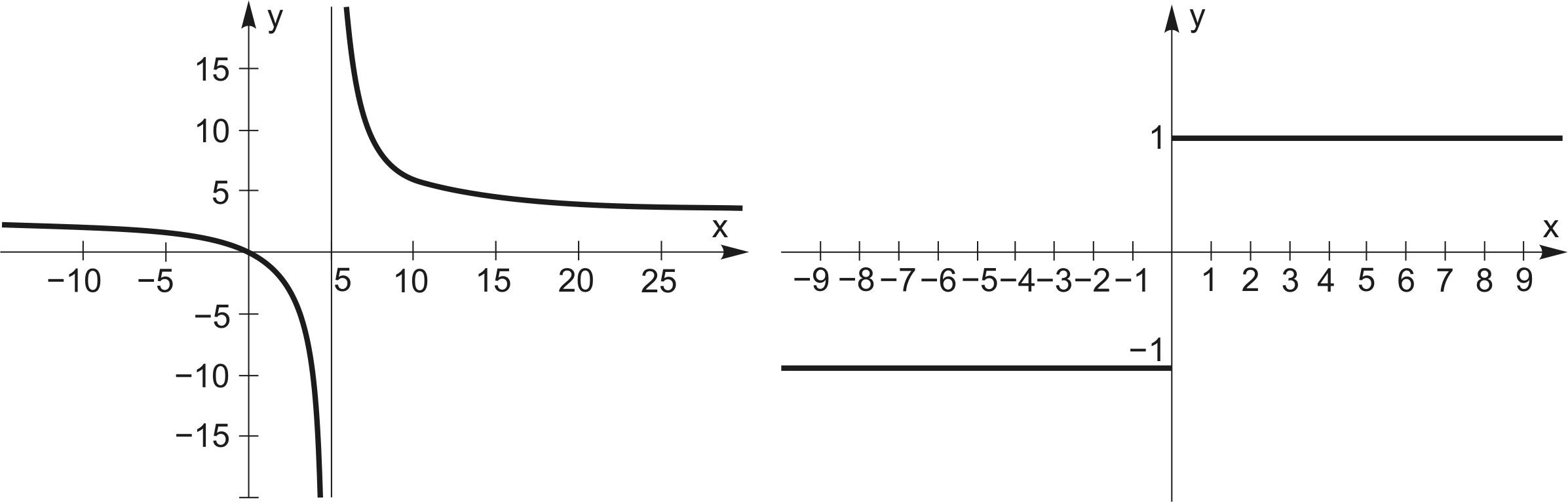
Рис. 4.4 Рис. 4.5
Приклад 4.2. Довести, що  має період
має період  .
.
Розв’язання. Відомо, що  де
де  , тому додавання
, тому додавання

Рис. 4.6 Рис. 4.7
 до аргументу синуса не змінює його значення. Чи є інше число з такою властивістю? Припустимо, що
до аргументу синуса не змінює його значення. Чи є інше число з такою властивістю? Припустимо, що  – таке число, тобто рівність
– таке число, тобто рівність  виконується для будь-якого значення
виконується для будь-якого значення  . Але тоді воно має місце і при
. Але тоді воно має місце і при  тобто
тобто  Однак за формулою зведення
Однак за формулою зведення  Тоді з двох останніх рівностей випливає, що
Тоді з двох останніх рівностей випливає, що  . Але це правильно лише при
. Але це правильно лише при  Оскільки найменшим відмінним від нуля числом з
Оскільки найменшим відмінним від нуля числом з  є
є  , то це число і є періодом
, то це число і є періодом  . Аналогічно можна довести, що
. Аналогічно можна довести, що  є періодом і для
є періодом і для  .
.
Приклад 4.3. Яке число є періодом функції  ?
?
Розв’язання. Оскільки  , то додавання
, то додавання  до аргументу
до аргументу  не змінює значення функції. Найменше відмінне від нуля число з
не змінює значення функції. Найменше відмінне від нуля число з  є
є  Таким чином, воно і є періодом
Таким чином, воно і є періодом  .
.
Обернена функція. Припустимо, що на проміжку  визначена функція
визначена функція  . Нехай область зміни цієї функції – проміжок
. Нехай область зміни цієї функції – проміжок  . Якщо для всіх
. Якщо для всіх 
рівняння  має лише один розв’язок, який належить проміжку
має лише один розв’язок, який належить проміжку  , то на проміжку
, то на проміжку  можна розглянути таку функцію
можна розглянути таку функцію  : для кожного
: для кожного  позначимо через
позначимо через  корінь рівняння
корінь рівняння  , тобто
, тобто  для всіх
для всіх  з проміжку
з проміжку  . Визначена так функція
. Визначена так функція  називається оберненою
називається оберненою  на проміжку
на проміжку  .
.
Якщо функція визначена на довільній множині  і кожного свого значення набуває тільки раз, то існує обернена
і кожного свого значення набуває тільки раз, то існує обернена  функція
функція  , визначена на всій області зміни функції
, визначена на всій області зміни функції  –
–  ; областю зміни
; областю зміни  є множина
є множина  .
.
Знаходження оберненої функції зводиться до розв’язування рівняння  відносно
відносно  .
.
Якщо одному значенню  з області зміни
з області зміни  відповідає кілька значень
відповідає кілька значень  , то обернена функція для
, то обернена функція для  на всій області визначення не існує, але
на всій області визначення не існує, але  має обернену функцію на кожному інтервалі монотонності.
має обернену функцію на кожному інтервалі монотонності.
Якщо функція  обернена до функції
обернена до функції  і
і  , то
, то  . Отже, якщо точка
. Отже, якщо точка  належить графіку функції
належить графіку функції  , то точка
, то точка  належить графіку функції
належить графіку функції  . Але ці дві точки симетричні відносно прямої
. Але ці дві точки симетричні відносно прямої  . Тому, щоб побудувати графік функції
. Тому, щоб побудувати графік функції  , оберненої до функції
, оберненої до функції  , треба графік функції
, треба графік функції  симетрично відобразити відносно бісектриси першого і третього координатних кутів. На рис. 4.8 зображено графіки обернених функцій
симетрично відобразити відносно бісектриси першого і третього координатних кутів. На рис. 4.8 зображено графіки обернених функцій  і
і  .
.
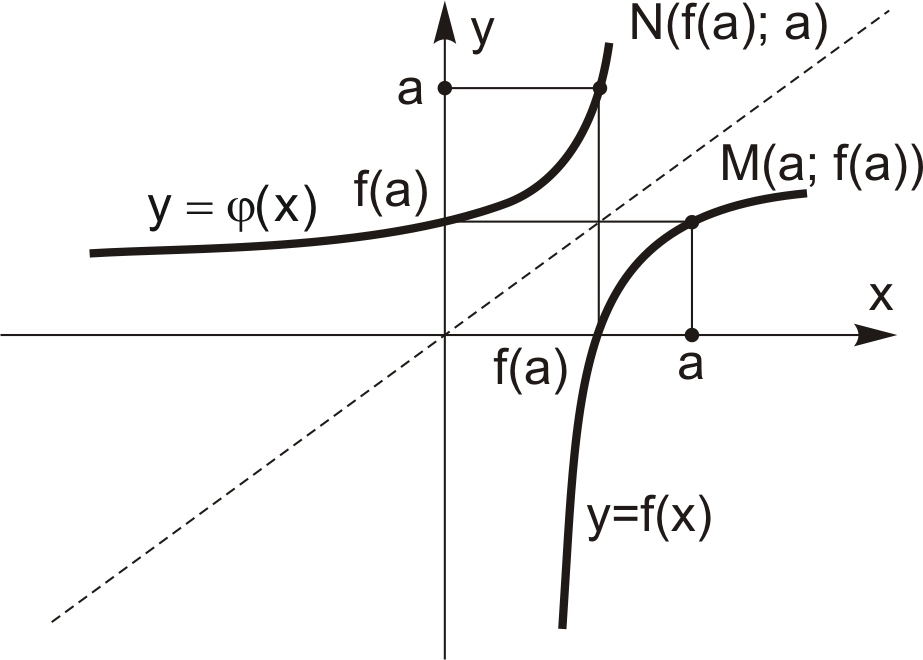
Рис. 4.8
Приклад 4.4. Записати функцію, обернену до функції  і побудувати її графік.
і побудувати її графік.
Розв’язання. Функція монотонна, тому обернена на всій області визначення, якою є множина дійсних чисел. Щоб скласти формулу оберненої функції, розв’яжемо рівняння  відносно змінної
відносно змінної  :
:  . Оскільки зазвичай ми позначаємо незалежну змінну –
. Оскільки зазвичай ми позначаємо незалежну змінну –  , а функцію –
, а функцію –  , то в отриманому виразі поміняємо місцями змінні. Функція
, то в отриманому виразі поміняємо місцями змінні. Функція  і є оберненою до даної. Графіки цих функцій наведено на рис. 4.9.
і є оберненою до даної. Графіки цих функцій наведено на рис. 4.9.
Складена функція. Розглянемо функцію  Фактично цей запис означає такий ланцюжок функціональних перетворень:
Фактично цей запис означає такий ланцюжок функціональних перетворень:
 .
.
У загальному вигляді останні перетворення можна записати так:
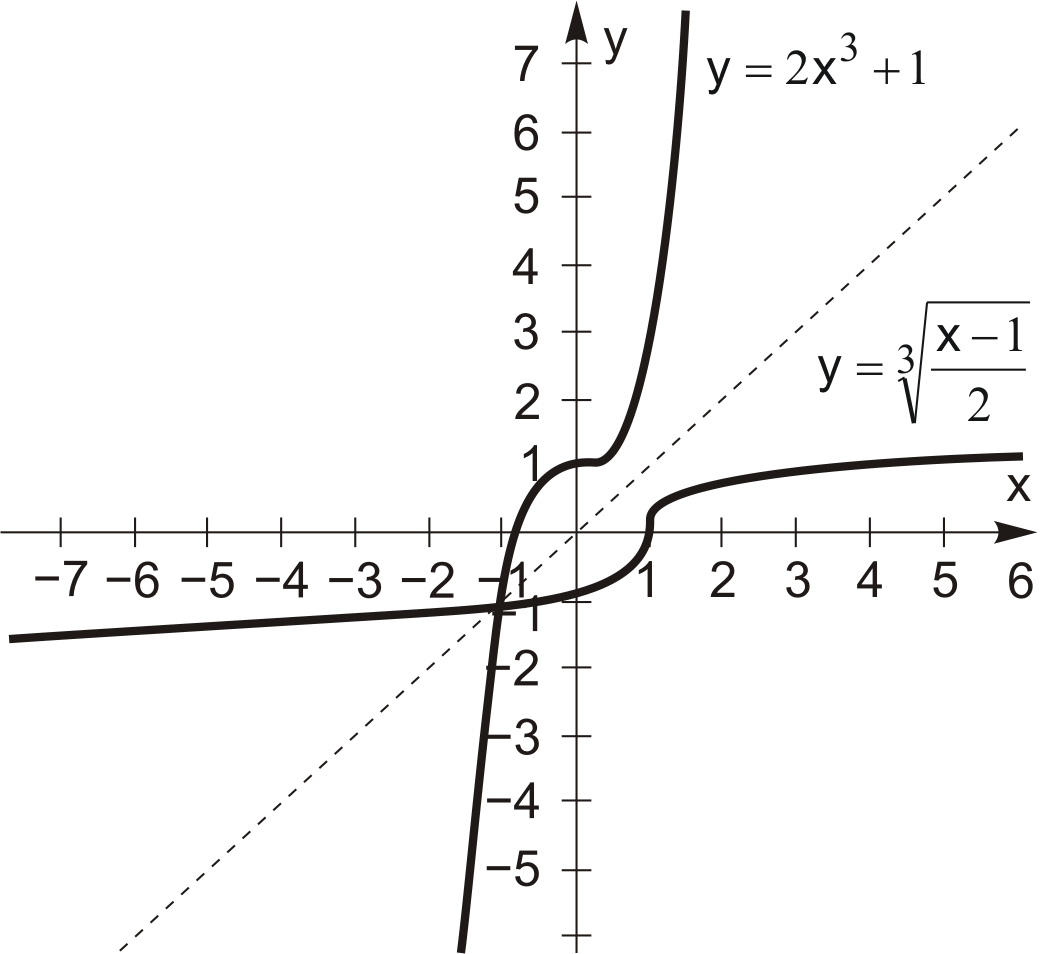
Рис. 4.9
 або
або 
Маємо два послідовних правила відповідності (тобто функції), використовуючи які отримаємо  як функцію від
як функцію від  . У цьому випадку говоримо, що
. У цьому випадку говоримо, що  – складена функція від
– складена функція від  .
.
Приклад 4.5. Наступні функції є складеними: 


Розв’язання. Ланцюжок перетворень для першої з них такий: 

 Для другої:
Для другої:  для третьої:
для третьої:  .
.
Графік функції. Графіком функції називається множина точок координатної площини, абсцисами яких є значення аргументу  з області визначення функції, а ординатами – значення функції
з області визначення функції, а ординатами – значення функції  з області значень.
з області значень.