Графіки алгебраїчних функцій

Лінійна функція. Функція вигляду називається лінійною функцією. Графіком функції є пряма лінія, яку можна побудувати за двома точками. Наприклад, якщо то , отже, – точка перетину з віссю ; якщо , то , маємо точку – точку перетину з віссю

Множник називається кутовим коефіцієнтом. Його геометричний зміст – , де – кут нахилу прямої до додатного напрямку осі (рис. 4.10).

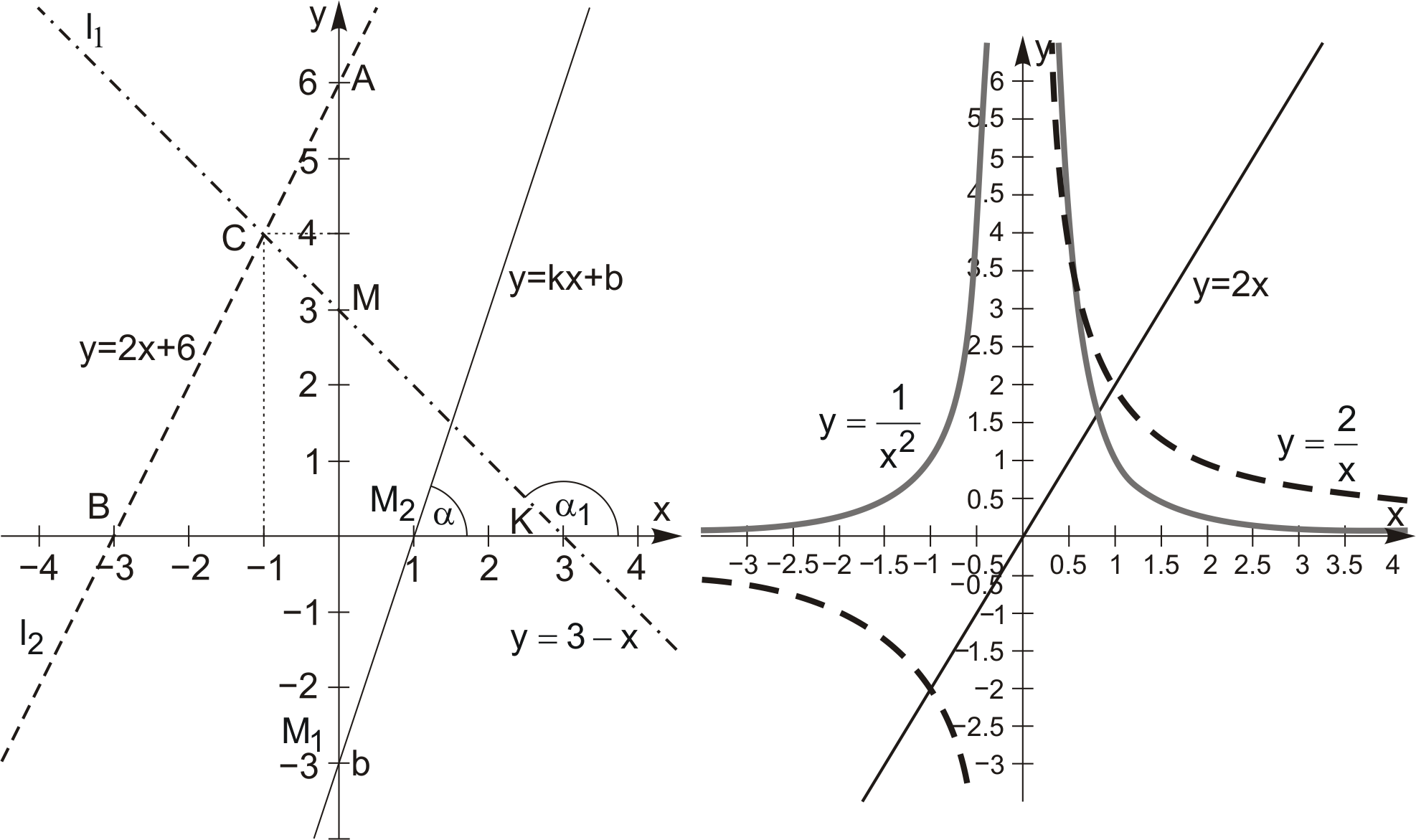
Рис. 4.10 Рис. 4.11

Приклад 4.6. Побудувати прямі і Знайти точку перетину прямих і кут нахилу прямої до осі

Розв’язання. 1) На : якщо то отже, – точка перетину з віссю ; якщо то отже, – точка перетину з віссю Таким чином, якщо відмітити точки і і провести через них пряму, то одержимо графік заданої функції . Аналогічно на маємо і – точки перетину відповідно з осями і Отже, з’єднуючи точки і , одержимо пряму (рис. 4.10). 2) Щоб знайти точку перетину двох графіків, треба прирівняти обидві функції: Розв’язком рівняння є Підставимо у будь-яке з рівнянь заданих прямих і одержимо ординату точки перетину Отже, – шукана точка. 3) Оскільки то

Пряма і обернена пропорційність. Найпростіший вигляд має рівняння прямої, яка проходить через початок координат: . Таке співвідношення між змінними і називається прямою пропорційністю, а число - коефіцієнтом пропорційності

(рис. 4.11, =2).

Співвідношення називається оберне ною пропорційністю. Графіком функції є гіпербола. Зазвичай гіперболу будують за точками. Оскільки функція є непарною, то спочатку будують одну гілку (для ), а другу будують симетрично початку координат. Прямі є асимптотами графіка (див. рис. 4.11, =2).

Приклад 4.7. Побудувати графік функції .

Розв’язання. Обчислимо кілька значень функції Таблиця 4.2

та запишемо їх для зручності у табл. 4.2. З

урахуванням симетрії та наявності асимптот будуємо

за точками задану криву (див.рис. 4.11).

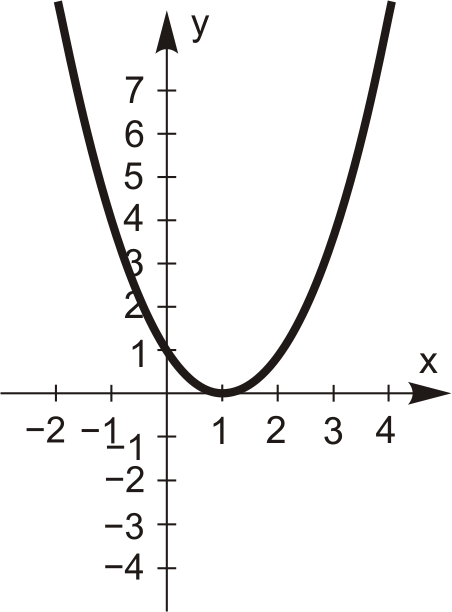
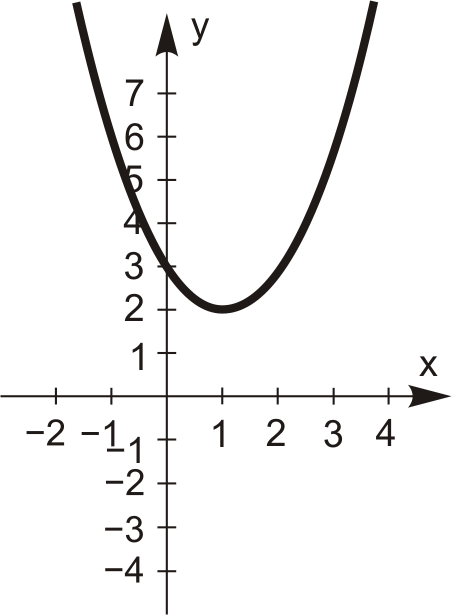
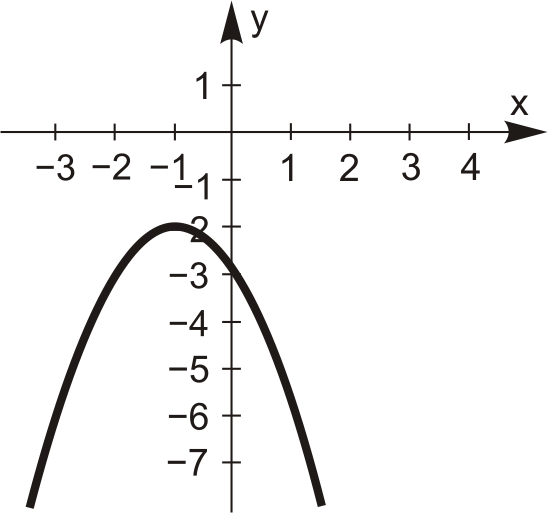
Квадратична функція. Функція вигляду називається квадратичною функцією. Її графіком є парабола. Залежно від коефіцієнта та дискримінанта графік цієї функції може мати вигляд, наведений у табл. 4.3.

Таблиця 4.3

Абсциси вершин	,

Степенева функція. Функція вигляду , де (довільна стала) – показник степеня, називається степеневою функцією від незалежної змінної . На рис. 4.12 наведено графіки степеневих функцій при деяких додатних значеннях , на рис. 4.11 – для від’ємних.

Аналізуючи графіки, які наведено на рис. 4.11 і 4.12, можна зазначити таке:

1) функції , , є частковими випадками степеневої функції;

2) коли , всі графіки проходять через точки (0; 0) і (1; 1);

3) якщо , то більшому значенню відповідає більше значення ;

Рис. 4.12

4) коли , то і лінії і є асимптотами графіка функції;

5) якщо – парне, то графік розташовано у І та ІІ чвертях, а якщо непарне – у І та ІІІ чвертях.

4.3. Графіки тригонометричних функцій

Основними тригонометричними функціями є функції , , , . Графіки цих функцій наведено на рис. 4.13 – 4.16.

Рис. 4.13

Рис. 4.14

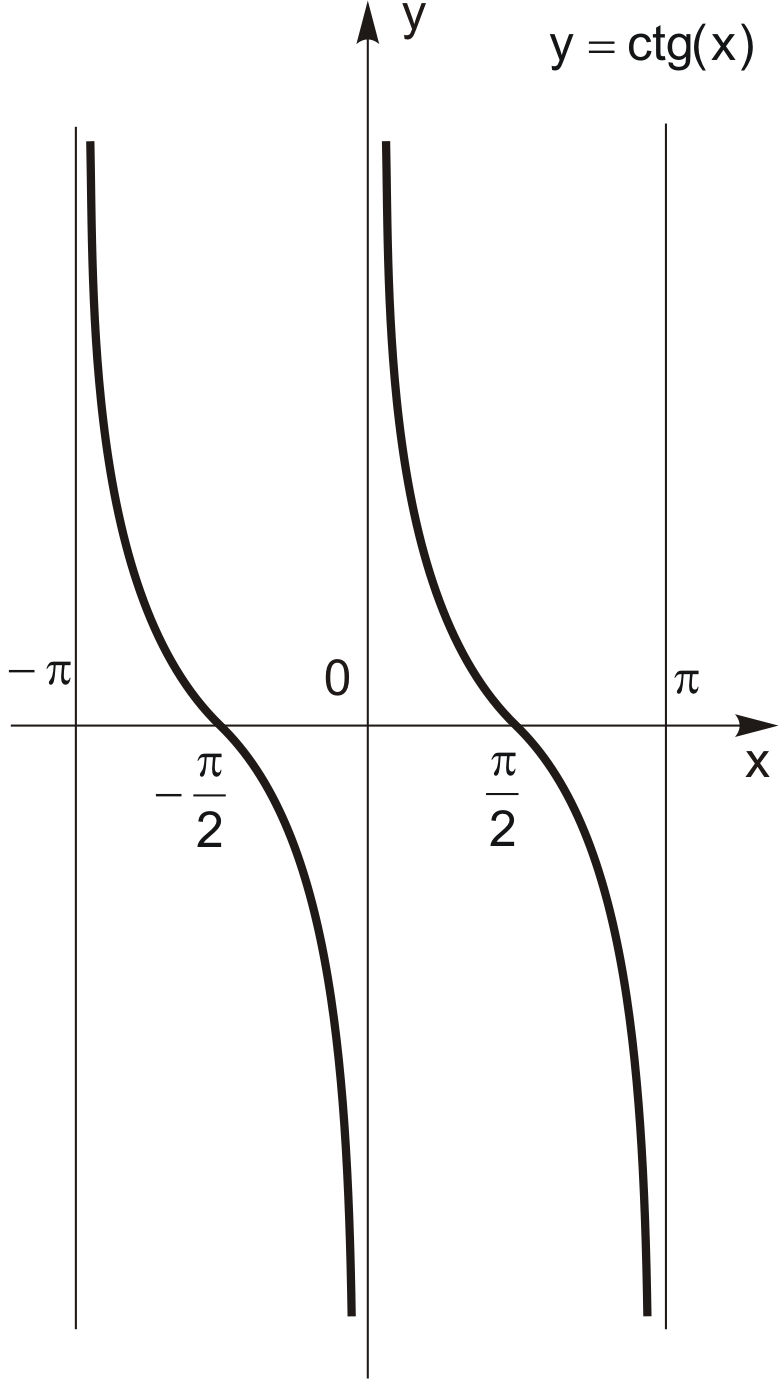
Рис. 4.15 Рис. 4.16