
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I Общие сведения
|
|
При всех своих достоинствах (простоте построения, возможности решать различные практические задачи) комплексный чертеж страдает одним существенным недостатком – он обладает малой наглядностью. Действительно, используя только комплексный чертеж (рис.1), без определенных усилий трудно вообразить себе даже столь простой оригинал, как срезанный параллелепипед (рис.2).

Рис.1 Рис.2
Поэтому во многих случаях, если необходимо полностью проявить конструктивное решение, лучше показать положение оригинала в пространстве, для чего обращаются к построению наглядных изображений.
В зависимости от конкретных условий, наглядные изображения выполняются в аксонометрических и аффинных проекциях, в линейной перспективе и др. Так, например, в архитектуре наибольшее распространение получили наглядные изображения, построенные в линейной перспективе и аксонометрии, в горном деле – в аффинных проекциях, а в машиностроении – в аксонометрических проекциях.
Что же такое аксонометрическая проекция?
Аксонометрия – греческое слово, состоящее из двух слов: acxon – ось и metreo – измеряю.
Сущность аксонометрического проецирования состоит в том, что оригинал совместно с пространственной системой координат проецируется в заданном направлении S на некоторую плоскость проекций П' (рис.3). В качестве проекционного аппарата чаще всего используется аппарат параллельного проецирования. Поэтому в дальнейшем под аксонометрическим чертежом будем понимать однокартинную параллельную проекцию оригинала, дополненную проекцией пространственной системы координат, к которой заранее был отнесен оригинал. Из этого следует, что аксонометрическая проекция обладает всеми свойствами параллельной проекции, а также обладает свойством обратимости по отношению к комплексному чертежу (т.е. позволяет воссоздать комплексный чертеж).

Рис. 3
В общем случае в процессе аксонометрического проецирования элементы оригинала искажаются. Степень их искажения зависит от положения плоскости аксонометрических проекций, направления проецирования и их положения относительно плоскости аксонометрических проекций. Определить заранее все множество степеней искажения невозможно. Поэтому выходит, что их необходимо определить хотя бы для направлений, параллельных координатным осям, а затем строить аксонометрическую проекцию оригинала по его отдельным точкам, применяя координатный метод.
Пусть, например, в пространственной системе координат задана точка А (рис.3). Ее положение определяется координатными отрезками Х, У, Ζ, которые, располагаясь цепочкой, образуют так называемую координатную ломаную. Выберем некоторую плоскость проекций П' и направление проецирования S и спроецируем точку А вместе с пространственной системой координат на эту плоскость. Получим аксонометрическую проекцию А' точки А, а также аксонометрические проекции Х'А, У'А, Ζ 'А ее
|
Величины координатных отрезков в аксонометрической и пространственной системе координат, можно связать постоянными, которые принято называть показателями (коэффициентами) искажения по осям:
kХ= Х'А: ХА; kУ=У'А: УА; kZ= Z'А: ZА.
Аксонометрическую проекцию, у которой все три коэффициента искажения равны, называют изометрической.
Если все коэффициенты не равны, то аксонометрическую проекцию называют триметрической.
Аксонометрическую проекцию, у которой два коэффициента искажения равны, называют диметрической.
Из конструкции аппарата параллельного проецирования следует, что величина коэффициентов искажения зависит от величины угла φ, который образует направление проецирования S с плоскостью аксонометрических проекций П'. Поэтому аксонометрические проекции принято делить на прямоугольные (φ =900) и косоугольные (φ ≠ 900).
Доказано, что в общем случае величины показателей искажения связаны между собой зависимостью:
kх2 + kу2 + kz2= 2 + ctg2φ.
Тогда для прямоугольных аксонометрических проекций приведенное равенство принимает вид:
kх2 + kу2 + kz2= 2.
Из приведенных формул следует, что при заданном направлении проецирования можно задаваться двумя произвольными коэффициентами искажения, но величина третьего из них будет определяться в соответствии с приведенными равенствами.
Если известно положение аксонометрических координатных осей X', Y', Z', а также величины коэффициентов искажения kх , kу, kz вдоль них, то порядок построения аксонометрической проекции А' некоторой точки А по ее комплексному чертежу будет следующим (рис.4):
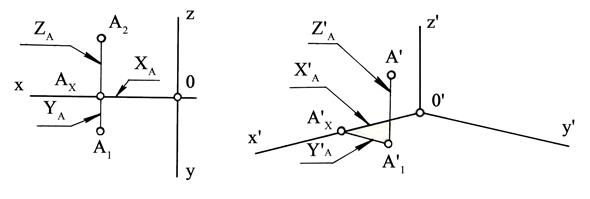
Рис. 4
Отложим вдоль аксонометрической координатной оси X' отрезок X'А=X∙ kх, из полученной точки проведем прямую, параллельную оси Y', и на ней отложим отрезок Y'А= Y ∙ kу . Получим так называемую вторичную проекцию А'1 точки А.
Из нее проведем прямую параллельную оси Z', и отложив на ней отрезок Z'А=Z∙ kZ , получим так называемую аксонометрическую проекцию А' точки А.
Построение аксонометрической проекции оригинала производится по отдельным точкам, которые соединяют между собой соответствующими линиями.
Поскольку при построении аксонометрических проекций используется метод параллельного проецирования, то аксонометрической проекцией прямой будет также прямая, а кривой – кривая. Поэтому для построения аксонометрической проекции отрезка прямой, достаточно построить аксонометрические проекции его концов и соединить их прямой, а для построения аксонометрической проекции отрезка кривой – построить аксонометрические проекции ряда принадлежащих ей точек и соединить их плавной кривой. При этом заметим, что аксонометрической проекцией окружности будет эллипс. Однако определить величины осей и их ориентацию относительно аксонометрических координатных осей возможно только для эллипсов, в которые проецируются окружности, параллельные основным плоскостям проекций.