Неопределенный интеграл. Основной задачей дифференциального исчисления является нахождение производной или дифференциала от данной функции.

Основной задачей дифференциального исчисления является нахождение производной или дифференциала от данной функции.

В интегральном исчислении основной задачей является обратная задача – отыскание функции по заданной ее производной 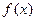или дифференциалу , т.е. для данной функции 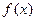надо найти такую функцию , что:

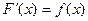или

Функция называется первообразной для функции 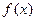на отрезке [a, b], если во всех точках этого отрезка выполняются равенства

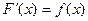или

Например, для функции 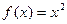первообразной будет функция

т.к.

Легко видеть, что если первообразная для функции 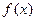, то функция 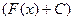тоже является первообразной для функции 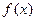, так как

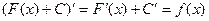
Если функция является первообразной для функции 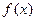, то выражение называется неопределенным интегралом от функции 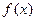и обозначается символом

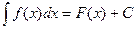
Функция 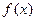называется подынтегральной функцией, – подынтегральным выражением, С – произвольная постоянная.

Нахождение первообразной для данной функции называется интегрированием.