Метод подведения под знак дифференциала.

Пусть требуется найти интеграл

где подынтегральные функции непрерывны. Применив подстановку , получим

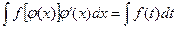
Полученная формула лежит в основе метода подведения под знак дифференциала. Покажем этот метод на примерах вычисления интегралов.

Например.

Найти интеграл
ы:

1.

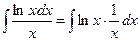
Обозначим , тогда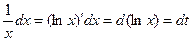

Следовательно

2.

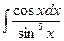
Обозначим , тогда 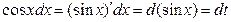Интеграл примет вид

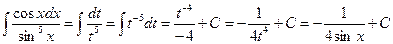
3.

4.

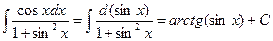
Преобразования подынтегральных выражений, проведенные в выше указанных интегралах, называются подведением под знак дифференциала.

Итак: Если подынтегральную функцию можно представить в виде произведения некоторой функции и производной от этой функции, либо от промежуточного аргумента этой функции, то, подведя под знак дифференциала производную, вычисление интеграла производится непосредственно.