
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства неопределенного интеграла.
|
|
1. Производная от неопределенного интеграла равна подынтегральной функции
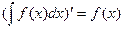
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.

Справедливость свойств 1 – 3 вытекает непосредственно из определения неопределенного интеграла.
4.Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов
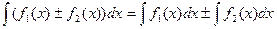
Для доказательства достаточно найти производные от левой и правой частей этого равенства


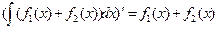

5. Постоянный множитель можно выносить за знак интеграла
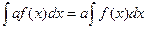
Для доказательства найдем производные от левой и правой частей равенства
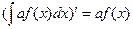

6. Если функция  является первообразной для функции
является первообразной для функции 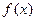 , то функция
, то функция
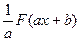 является первообразной для функции
является первообразной для функции 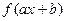 , то есть, если
, то есть, если 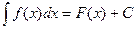 , то
, то 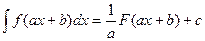
Для доказательства найдем производные от левой и правой частей равенства
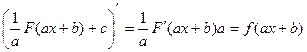
Таблица интегралов.

Таблица интегралов получается непосредственно из определения неопределенного интеграла и таблицы производных. Для установления справедливости указанных в таблице формул достаточно найти производные от правых частей равенств и получить подынтегральные функции.
1. 
2. 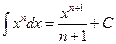
3. 
4. 
5. 
6. 
7. 
8. 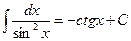
9. 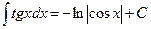
10. 
11. 
12. 
13. 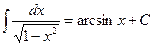
14.
15. 
16. 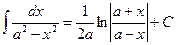
Заметим, что функций, стоящих в правых частях последних формул нет в таблице производных. Однако, эти интегралы часто встречаются в практических задачах, поэтому они помещены в таблицу. Справедливость их нетрудно проверить непосредственным дифференцированием функций, стоящих в правых частях равенств.
Например, формула 12 доказывается так:

Аналогично проверяются остальные формулы.