
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Integrating Factors
|
|
When the equation
Pdx + Qdy = 0 (1)
is not exact, we may seek to make it exact by multiplying throughout by a suitable notation μ (x, y). Applying the condition for the equation
(μ P)dx + (μ Q)dy = 0
to be exact, we see that such a function μ must satisfy the equation
 (2)
(2)
If we can find a function μ which satisfies this equation, we may say that we have found an integrating factor of the equation (1).
It is not an easy matter to find functions which satisfy equation (2) unless we make some simplifying assumption about the nature of μ. μ is a function of x alone. If we assume that μ = μ (x) is a function of x alone,
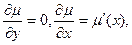
the equation (2) reduces to
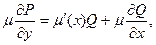
which may be written in the form
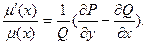 (3)
(3)
Now the function on the left-hand side of this equation contains x alone and this must therefore also be true of the function on the right-hand side of this equation. Our assumption that μ is a function of x alone is justified, therefore, only if it turns out that 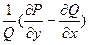
is a function of x alone. If we denote this function by ψ (x), equation (3) may be put in the form 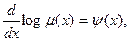
showing that log μ (x)= ∫ ψ (x)dx (4)
is an equation from which we can easily determine μ (x).
*Source: J.G.Deferes and Sheddon The Mathematics of Medicine and Biology, p.446-447.