Text 2.

Review.

We begin by recalling the definition of a first-order differential equation. Consider an equation F (x, y, z)=0 in which not all the variables need occur, but at least z does. The equation

(1)

obtained by substituting 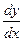for z, is a first-order differential equation. By a solution of (1) is meant any differentiable function f for which the equation

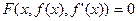
is true for every x in the domain of f. If f is a solution, we write

.

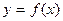The general problem, given a differential equation, is to find all its solutions. A more specialized problem is to find a particular solution y=f(x) which has a specified value b at some specified number a, i.e., a solution for which b=f(a).

The simplest first-order differential equations are those of the type where f is some given function. Every solution of this differential equation can be written

y=∫ f(x)dx+c,

for some real number c. Hence if c is left as an arbitrary undetermined constant of integration, we call ∫ f(x)dx+c the general solution.

We next considered differential equations of the form 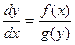, in which f and g are given functions. Equations of this type are called separable, since, if we use the fact that the derivative is equal to the ratio of two differentials, we can “separate” the expression containing x from that containing y by writing the equivalent differential equation

g(y)dy=f(x)dx.

Integrating both sides, we get the equation

∫ g(y)dy= ∫ f(x)dx+c,

which defines the general solution y implicitly as a function of x. Note that the differential equation 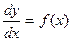discussed above is a separable equation in which g(y) = 1.

Of special interest among separable equations is the first-order linear differential

equation 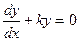, in which k is a constant. This is the type of differential equation which describes the rate of decay of a radioactive substance and also the rate of growth of bacteria in a culture. It can be solved without difficulty as a separable differential equation. However, this equation occurs sufficiently often and has such an obvious general solution that most people recognize it at sight. The general solution is y=ce^-kx.

*Source: Crowell and Slesnick's Calculus with Analytic Geometry The Dartmouth CHANCE Project Version 3.0.3, 5 January 2008

Comprehension questions:

1) What is a first-order differential equation?

2) What is a general problem for differential equations?

3) What is a more specialized problem?

4) What equations are referred to as separable?

5) What does it mean to define the solution implicitly?

6) Why are some separable equations of special interest?