Translate the following paragraphs into English. Числа – это неотъемлемое орудие современной цивилизации, используемое для упорядочения сферы ее деятельности

Числа – это неотъемлемое орудие современной цивилизации, используемое для упорядочения сферы ее деятельности. В наиболее примитивном применении числа служат опознавательными знаками, будь то телефонные номера, номера автомашин или числа почтового индекса. На этом уровне мы просто сравниваем одно число с другим, не подвергая их арифметическим операциям. Вряд ли можно ожидать, что получится что-либо значимое, если сложить номера телефонов Леонарда Бернстейна и Элизабет Тэйлор. На следующей, чуть более сложной ступени, мы извлекаем пользу из естественного порядка положительных целых чисел, например, когда запоминаем номер нашей очереди или когда на скачках записываем наездников, приходящих к финишу. Здесь мы еще не нуждаемся в операциях над числами; все, что нас интересует – это больше или меньше одно число, чем другое. Арифметика в полном смысле этого слова появляется, лишь когда задают себе вопрос: «Сколько?» Вот здесь нас уже ждут трудности вычитания, сложения, умножения, деления, извлечения квадратных коней и еще более замысловатых операций над числами.

Иррациональные числа казались грекам парадоксальными, ибо они не могли представить себе числа, которые не были бы ни целыми, ни отношениями двух целых. Тем не менее, греки представляли эти числа геометрически. В прямоугольном треугольнике с катетами 3 и 4 гипотенуза равна 5 единицам. Но никакая рациональная дробь не выражает 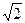, т.е. длину гипотенузы прямоугольного треугольника с катетами по одной единице длины каждый. Получилось, что некоторая линия вполне ощутимой длины, которую можно легко построить, тем не менее оказывалась «неизмеримой».

***

Part 2

In the 19^th century mathematicians invented several new number systems. Of these modern systems three are particularly noteworthy: quaternions, matrices and transfinite numbers.

Quaternions were Hamilton’s great creation. For many years he brooded over the fact that the multiplication of complex numbers has a simple interpretation as the rotation of a plane. Could this idea be generalized? Would it be possible to invent a new kind of number and to define a new kind of multiplication such that a rotation of three-dimensional space would have a simple interpretation in terms of the multiplication? Hamilton called such a number a triplet; just as Wessel represented complex numbers by a point on a two-dimensional plane, the triplets were to be represented by a point in three-dimensional space.

The problem was a hard nut to crack. It was continually on Hamilton’s mind, and his family worried over it with him. As he himself related, when he came down to breakfast, one of his sons would ask, “Well, Papa, can you multiply triplets? ” And Papa would answer dejectedly, “No, I can only add and subtract them.”

One day in 1843, while he was walking with his wife along a canal in Dublin, Hamilton suddenly conceived a way to multiply triplets. He was so elated that he took out a penknife then and there and carved on Brougham Bridge the key to the problem, which certainly must have mystified passersby who read it: “i²=j²=k²=ijk= -1.”

The letters i, j, k represent hyper-complex numbers Hamilton called quaternions (the general form of a quaternion being a+bi+cj+dk, with a, b, c and d denoting real numbers). Just as the square of 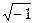² is -1, so i²= -1, j²= -1 and k²= -1 The key to the multiplication of quaternions, however, is that the commutative law does not hold. Whereas in case of ordinary numbers ab=ba, when quaternions are reversed, the product may be changed, for example, ij=k, but ji= -k.

The second modern number concept mentioned above, that of the matrix, was developed more or less simultaneously by Hamilton and the British mathematicians J.J. Sylvester and Arthur Cayley. A matrix can be regarded as a rectangular array of numbers. For example, 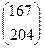is a matrix. The entire array is thought of as an entity in its own right. Under the proper circumstances it is possible to define operations of addition, subtraction, multiplication and division for such entities. The result is a system of objects whose behavior is somewhat reminiscent of ordinary numbers and which is of great utility in many provinces of pure and applied mathematics.

The third modern concept, that of transfinite numbers, represents a totally different order of idea. It is entertainingly illustrated by a fantasy, attributed to the noted German mathematician David Hilbert and known as “Hilbert’s Hotel”. It would be appreciated by roomless visitors to the New York World’s Fair. A guest comes to Hilbert’s Hotel and asks for a room. “Hmm, ” says the manager, “we are all booked up, but that’s not an unsolvable problem here; we can make space for you.” He puts the new guest in room 1, moves the occupant of room 1 to room 2, the occupant of room 2 to room 3 and so on. The occupant of room N goes into room N+1. The hotel simply has an infinite number of rooms.

How, then, can the manager say that the hotel is “all booked up”? Galileo noted a similar paradox. Every integer can be squared, and from this we might conclude that there are as many squares as there are integers. But how can this be, in view of the known fact that there are integers that are not squares, for instance, 2, 3, 5, 6…?

One of the endlessly alluring aspects of mathematics is that its thorniest paradoxes have a way of blooming into beautiful theories. The 19^th century German mathematician Georg Cantor turned this paradox into a new number system and an arithmetic of infinite numbers.

He started by defining an infinite set as one that can be put into a one-to-one correspondence with a part of itself, just as the integers are in a one-to-one correspondence with their squares. He noted that every set that can be put into such correspondence with the set of all the integers must contain an infinite number of elements, and he designated this number as 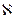(aleph, the first letter of the Hebrew alphabet). Cantor gave this “first transfinite cardinal” the subscript zero. He then went on to show that there is an infinity of other sets (for example, the set of real numbers) that cannot be put into a one-to-one correspondence with the positive integers because they are larger than that set. Their sizes are represented by other transfinite cardinal numbers ( 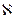₁, 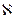₂ and so on). From such raw materials Cantor developed an arithmetic covering both ordinary and transfinite numbers. In this arithmetic some of the ordinary rules are rejected, and we get strange equations such as 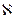₀+1= 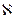₀. This expresses, in symbolic form, the hotel paradox.

The transfinite numbers have not yet found application outside mathematics itself. But within mathematics they have had considerable influence and have evoked much logical and philosophical speculation. Cantor’s famous “continuum hypothesis” produced a legacy of unsolved problems that still occupy mathematicians. In recent years solutions to some of these problems have been achieved by Alfred Tarski of the University of California at Berkeley and Paul J. Cohen of Stanford University.

***