Example 3.

Find the particular solution of the differential equation D(D-5)y = 0 which has value equal to 2 and derivative equal to -15 when x = 0. The characteristic equation is t(t - 5) = 0, whose roots are obviously 0 and 5. The general solution is therefore

y=c₁e^0x+c₂e^5x=c₁+c₂e^5x

The derivative is y’=5c₂e^5x.

When x = 0, we are told that y = 2 and y’ = -15. Substituting these values in the preceding equations, we obtain

2=c₁+c₂e^5.0=c₁+c₂

-15=5c₂e^5.0=5c₂.

It follows that c₂ = -3 and thence that c₁ = 5. Hence the required solution is

y=5-3e^5x.

It is extremely useful to recognize alternative forms of the general solution of the differential equation (D² + aD + b)y = 0 in the case where the roots of the characteristic equation are the complex numbers α + iβ and α - iβ. In particular, it is easy to verify that the functions

y=ce^{α x}sin(β x+k), (1)

y=ce^{α x}cos(β x+k) (2)

where c and k are arbitrary real numbers, are both solutions. To see that this is so, we expand (1) using the trigonometric identity for the sine of the sum of two numbers. The result is

y = ce^{α x}(sin β x cos k + cos β x sin k)

= e^{α x}[(c sin k) cosβ x + (c cos k) sinβ x].

Setting c₁ = c sin k and c₂ = c cos k, we obtain y = e^{α x} (c₁ cosβ x+c₂ sinβ x), which we know to be a solution. The proof for (2) is analogous.

Conversely, any solution y = e^{α x} (c₁ cosβ x+c₂ sinβ x) can be written in the forms (1) and (2). For if both c₁ = c₂ = 0, then y = 0, and we need only set c = 0 in (1) and (2). If c₁ and c₂ are not both zero, then 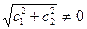, and we can write

y= e^{α x}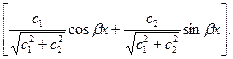

To put this equation in the form of (1), we set c = and observe that, since 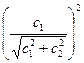= 1

it follows from our definition of the functions sine and cosine that there exists a real number k such that cos k = and sin k= . Hence, we get

y = ce^{α x}(sin k cos β x + cos k sin β x)

= ce^{α x}sin (β x +k).

Again, by an analogous argument, the solution can also be written in the form of equation (2).

An advantage in using the forms (1) and (2) for the general solution is that it is easy to see what the graphs of such functions look like. They are all sinusoidal curves lying between the graphs of y = ce^{α x} and y = - ce^{α x}.

Give the English equivalents for: получить; производная; равный; подставить эти значения; корни характеристического уравнения; требуемое решение; доказать; доказательство; произвольные вещественные числа; наблюдать; можно записать; кривые.

Grammar Notes: