Text 1.

“One of the endlessly alluring aspects of mathematics is

that its thorniest paradoxes have a way of blooming into beautiful theories.”

Philip J. Davis

Source: Number, Scientific American, 211, (Sept. 1964), 51 - 59.

Part 1

By popular definition a mathematician is a fellow who is good at numbers. Most mathematicians demur. They point out that they have as much difficulty as anybody else in reconciling their bank statements, and they like to refer to supporting anecdotes, such as that Isaac Newton, who was Master of the Mint, employed a bookkeeper to do his sums. They observe further that slide rules and electronic computers were developed as crutches to help mathematicians.

All of this is obviously irrelevant. Who, if not the mathematician, is the custodian of the odd numbers and the even numbers, the square numbers and the round numbers? To what other authority shall we look for information and help on Fibonacci numbers, Liouville numbers, hypercomplex numbers and transfinite numbers? Let us make no mistake about it: mathematics is and always has been the number game par excellence. The great American mathematician G.D.Birkhoff once remarked that simple conundrums raised about the integers have been a source of revitalization for mathematics over the centuries.

The complexity of a civilization is mirrored in the complexity of its numbers. Twenty-five hundred years ago the Babylonians used simple integers to deal with the ownership of a few sheep and simple arithmetic to record the motions of the planets. Today mathematical economists use matrix algebra to describe the interconnections of hundreds of industries and physicists use transformations in “Hilbert space” – a number concept seven levels of abstraction higher than the positive integers – to predict quantum phenomena.

The number systems employed in mathematics can be divided into five principal stages, going from the simplest to the most complicated. They are: (1) the system consisting of the positive integers only; (2) the next higher stage, comprising the positive and negative integers and zero; (3) the rational numbers, which include fractions as well as the integers; (4) the real numbers, which include the irrational numbers, such as π; (5) the complex numbers, which introduce the “imaginary” number .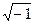

The positive integers are the numbers a child learns in counting. They are usually written 1, 2, 3, 4, …, but they can and have been written in many other ways. The Romans wrote them I, II, III, IV, …; the Greeks wrote them α, β, γ, δ …; in the binary number system, containing only the digits 0 and 1, the corresponding numbers are written as 1, 10, 11, 100… All these variations come to the same thing: they use different symbols for entities whose meaning and order are uniformly understood.

Early man needed only the first few integers, but with the coming of civilization he had to invent higher and higher numbers. This advance did not come readily. As Bernard Shaw remarked in “Man and Superman”, “To the Bushman who cannot count further than his fingers, eleven is an incalculable myriad.” As late as the third century B.C. there appears to have been no systematic way of expressing large numbers. Archimedes then suggested a cumbersome method of naming them in his work “The Sand Reckoner”.

Yet while struggling with the names of large numbers, the Greek mathematicians took the jump from the finite to the infinite. The jump is signified by the three little dots placed after the 4 in the series above. They indicate that there is an integer after 4 and another after the successor to 4 and so on through an unlimited number of integers. For the ancients this concept was a supreme act of the imagination, because it ran counter to all physical experience and to a philosophical belief that the universe must be finite. The bold notion of infinity opened up vast possibilities for mathematics, and it also created paradoxes. Its meaning has not been fully plumbed to this day.

Oddly the step from the positive to the negative integers proved to be a more difficult one to make. Negative numbers seem altogether commonplace in our day, when 10 degrees below zero is a universally understood quality and the youngest child is familiar with the countdown “…five, four, three, two, one….” But the Greeks dealt with negative numbers only in terms of algebraic expressions of the areas of squares and rectangles, for example (a-b) ²= a²-2ab+b². Negative numbers were not fully incorporated into mathematics until the publication of Girolamo Cardano’s “Ars Magna” in 1545.

Fractions, or rational numbers (the name they go by in number theory), are more ancient than the negative numbers. They appear in the earliest mathematical writings and were discussed at some length as early as 1550 B.C. in the Rhind Papyrus of Egypt. The present way of writing fractions (for instance 1/4, 1/5, 8/13) and also the present way of doing arithmetic with them date from the 15^th and 16^th centuries.

The irrational numbers also have a long history. In the sixth century B.C. the mathematical school of Pythagoras encountered a number that could not be fitted into the category of either integers or fractions. This number, arrived at by the Pythagorean theorem, was 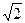: the length of the diagonal of a square (or the hypotenuse of a right triangle) whose sides are one unit long. The Greeks were greatly upset to find that 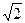could not be expressed in terms of any number a/b in which a and b were integers, that is, any rational number. Since they originally thought the only numbers were rational numbers, this discovery was tantamount to finding that the diagonal of a square did not have a mathematical length! The Greeks resolved this paradox by thinking of numbers as lengths. This led to a program that inhibited the proper development of arithmetic and algebra, and Greek mathematics ran itself into a stone wall.

It took centuries of development and sophistication in mathematics to realize that the square root of two can be represented by putting three dots after the last calculated digit. Today we press the square-root button of a desk calculator and get the answer: 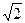=1.41421… Electronic computers have carried the specification of the digits out to thousands of decimal places. Any number that can be written in this form – with one or more integers to the left of a decimal point and an infinite sequence of integers to the right of the point – is a “real” number. We can express in this way the positive integers (for example, 17=17.0000…), the negative integers (-3=-3.0000…) or the rational numbers (17 1/5=17.20000…). Some rational numbers do not resolve themselves into a string of zeroes at the right; for instance, the decimal expression of one seventh is 1/7=0.142857 142857 142857… What makes these numbers “rational” is the fact that they contain a pattern of digits to the right of the decimal point that repeats itself over and over. The numbers called “irrational” are those that, like the square root of two, have an infinitely non-repeating sequence of decimal digits. The best-known examples of irrational are: 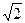=1.4142135623… and π =3.1415926535… The irrational numbers are of course included among the real numbers.

It is in the domain of the “complex numbers” that we come to the numbers called “imaginary” – a term that today is a quaint relic of a more naï ve, swashbuckling era in arithmetic. Complex numbers feature the “quantity” 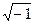, which, when multiplied by itself, produces -1. Since this defies the basic rule that the multiplication of two positive or negative numbers is positive, 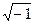(or i, as it is usually written) is indeed an oddity: a number that cannot be called either positive or negative. “The imaginary numbers, ” wrote Gottfried Wilhelm von Leibniz in 1702, “are a wonderful flight of God’s Spirit; they are almost an amphibian between being and not being.”

From Renaissance times on, although mathematicians could not say what these fascinating imaginaries were, they used complex numbers (which have the general form a+b 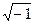) to solve equations and uncovered many beautiful identities. Abraham de Moivre discovered the formula

(cos θ + 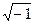sinθ)ⁿ=cos nθ + 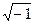sin nθ.

Leonard Euler discovered the related formula

e^π 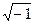= - 1

(e being the base of the “natural logarithms”, 2.71828…).

The complex numbers remained on the purely manipulative level until the 19^th century, when mathematicians began to find concrete meanings for them. Caspar Wessel of Norway discovered a way to represent them geometrically, and this became the basis of a structure of great beauty known as the theory of functions of a complex variable. Late the Irish mathematician William Rowan Hamilton developed an algebraic interpretation of complex numbers that represented each complex number by a pair of ordinary numbers. This idea helped to provide a foundation for the development of an axiomatic approach to algebra.

Meanwhile physicists found complex numbers useful in describing various physical phenomena. Such numbers began to enter into equations of electrostatics, hydrodynamics, aerodynamics, alternating-current electricity, diverse other forms of vibrating systems and eventually quantum mechanics. Today many of the productions of theoretical physics and engineering are written in the language of the complex-number system.

***