Translate the following paragraphs into English.

Таблица для умножения кватернионов, предложенная У.Гамильтоном, раскрывает некоммутативную природу этих новых мнимых величин. Если, например, j из строки умножить на k из столбца, то получится i, но если k из строки умножить на j из столбца, то в ответе будет уже -i. Каждая из этих трех величин, умноженная сама на себя, дает -1.

Матрицы – это прямоугольные таблицы чисел, сами по себе не имеющие численного значении, но с которыми тем не менее можно обращаться как с некими сущностями, по определенным правилам их складывать, вычитать, умножать и делить. Такие таблицы дают удобный способ для вычисления одновременных изменений в ряде связанных друг с другом переменных. Любые две матрицы с одинаковым числом строк и столбцов можно складывать. Сложение матриц производится строка за строкой, причем каждый элемент каждого столбца первой матрицы прибавляется к соответствующему элементу второй. Таким образом получается новая матрица. Умножение матриц – более сложный процесс, для которого две матрицы уже не обязаны быть одного размера. Матрица размером 2х3 может быть умножена на матрицу размером 3х2. Каждый член верхней строки левой матрицы последовательно умножается на соответствующий член первого столбца правой матрицы; сумма этих умножений и есть то число, которое ставится в первую строку и первый столбец матрицы-результата. Верхняя строка левой матрицы служит теперь для того, чтобы тем же способом вместе со вторым столбцом правой матрицы составить число для второго столбца первой строки матрицы-результата. Затем верхняя строка левой матрицы умножается на третий столбец правой матрицы. И все это повторяется снова для каждой из строк левой матрицы.

Существует бесчисленное множество трансфинитных количественных чисел. Наиболее известное из них 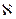₀ символизирует число или количество положительных целых чисел или элементов любого множества, которое может быть поставлено во взаимно однозначное соответствие с множеством всех положительных целых чисел. Такие множества называют счетными. Количество всех действительных чисел больше, чем одних только положительных целых, и эквивалентно количеству всех точек на прямой, на плоскости или в любом «куске» пространства более высокой размерности. Эти уже несчетные множества обозначают символом 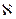₁. Число всех возможных точечных множеств есть еще большее трансфинитное количественное число - 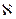₂.

***

Part 3

We have reviewed the subject matter (or dramatis personae) of the numbers game; it now behooves us to examine the rules of the game. To non-mathematicians this may seem to be an exercise in laboring the obvious. The geometry of Euclid is built on “self-evident” axioms, but rigorous examination of the axioms in the 19^th century disclosed loopholes, inconsistencies and weaknesses that had to be repaired in order to place geometry on firmer foundation. But, one may ask, what is there about the simple rules of arithmetic and algebra that needs examination or proof? Shaken by the discoveries of the shortcomings of Euclid’s axioms, and spurred by the surprising features of the new number concepts such as the quaternions, many mathematicians of the 19^th century subjected the axioms of number theory to systematic study.

Are the laws of arithmetic independent, or can one be derived logically from another? Are they really fundamental, or could they be reduced to a more primitive, simpler and more elegant set of laws? Answers to questions such as these have been sought by the program of axiomatic inquiry, which is still going on. It has yielded rigorous and aesthetically appealing answers to some of them, and in the process it has brought forth new concepts such as “rings”, “fields”, “groups” and “lattices”, each with its own set of rules of operation and its own characteristic theory.

One of the major accomplishments, achieved in the 1870’s, was the establishment of a set of axioms for the real numbers. It is summed up in the statement that the real-number system is a “complete ordered field”. Each of these words represents a group of rules that defines the behavior of the numbers.

First of all, the word “field” means a mathematical system in which addition and multiplication can be carried out in a way that satisfies the familiar rules, namely (1) the commutative law of addition: x+y=y+x; (2) the associative law of addition: x+(y+z)=(x+y)+z; (3) the commutative law of multiplication: xy=yx; (4) the associative law of multiplication: x(yz)=(xy)z; (5) the distributive law: x(y+z)=xy+xz.

Furthermore, a field must contain a zero element, 0, characterized by the property that x+0=x for any element x. It contains a unit element 1, that has the property that 1 • x=x. For any given element x of a field there is another element -x such that –x+x=0. This is the foundation on which subtraction is built. Another axiomatic property of a field is the cancellation rule of multiplication, that is, if xy=xz, then y=z (provided that x is not equal to zero). Finally, for any element x (other than zero) afield must contain an element 1/x such that x(1/x)=1. This is the basis for division. Briefly, then, a field is a system (exemplified by the rational numbers) whose elements can be added, subtracted, multiplied and divided under the familiar rules of arithmetic.

Considering now the second word, a field is “ordered” if the sizes of its elements can be compared. The shorthand symbol used to denote this property is the sign >, meaning “greater than”. This symbol is required to obey its own set of rules, namely (1) the trichotomy law: for any two elements x and y, exactly one of these three relations is true, x> y, x=y or y> x; (2) the transitivity law: if x> y and y> z, then x> z; (3) the law of addition: if x> y, then x+z> y+z; (4) the law of multiplication: if x> y and z> 0, then xz> yz.

Finally, what do we mean by the word “complete” in describing the system of real numbers as a “complete ordered field”? This has to do with the problem raised by a number such as 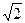. Practically speaking, 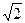is given by a sequence of rational numbers such as 1, 1.4, 1.41, 1.414… that provide better and better approximations to it. That is to say, 1²=1, (1.4)²=1.96, (1.41)²=1.9981, (1.414)²=1.999396… Squaring these numbers yields a sequence of numbers that are getting closer and closer to 2. Notice, however, that the numbers in the original sequence (1, 1.4, 1.41…) are also getting closer and closer to one another. We would like to think of 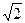as the “limiting value” of such a sequence of approximations. In order to do so we need a precise notion of what is meant by saying that the numbers of a sequence are getting closer and closer to one another, and we need a guarantee that our system of numbers is rich enough to provide us with a limiting number for such a sequence.

Following the path taken by Cantor, we consider a sequence of numbers in our ordered field. We shall say that the numbers of this sequence are getting closer and closer to one another if the difference of any two numbers sufficiently far out in the sequence is as small as we please. This means, for example, that all terms sufficiently far out differ from one another by at the most 1/10. If one wishes to go out still further, they can be made to differ by at most 1/100, and so forth. Such a sequence of numbers is called a “regular sequence”. An ordered field is called a “complete” ordered field if, corresponding to any regular sequence of elements, there is an element of the field that the sequence approaches as a limiting value. This is the “law of completeness”: the “gaps” between the rational numbers have been completed, or dilled up. It is the final axiomatic requirement for the real-number system.

All these rules may seem so elementary that they hardly need stating, let alone laborious analysis. The program of systematizing them, however, has been vastly rewarding. Years of polishing the axioms have reduced them to a form that is of high simplicity. The rules I have just enumerated have been found to be necessary, and sufficient, to do the job of describing and operating the real-number system; throw any one of them away and the system would not work. And, as I have said, the program of axiomatic inquiry has answered some fundamental questions about numbers and produced enormously fruitful new concepts.

The spirit of axiomatic inquiry pervades all modern mathematics; it has even percolated into the teaching of mathematics in high schools. A high school teacher recently said to me, “In the old days the rules of procedure were buried in fine print and largely ignored in the classroom. Today the fine print has been parlayed into the main course. The student is in danger of knowing that 2+3=3+2 by the commutative law but not knowing that the sum is 5.” Of course, anything can be overdone. Exclusive attention to axiomatics would be analogous to the preoccupation of a dance group that met every week and discussed choreography but never danced. What is wanted in mathematics, as in anything else, is a sound sense of proportion.

***

Part 4

We have been considering how numbers operate; ultimately we must face the more elementary question: What are numbers, after all? Nowadays mathematicians are inclined to answer this question too in terms of axiomatics rather than in terms of epistemology or philosophy.

To explain, or better still to create, numbers it seems wise to try the method of synthesis instead of analysis. Suppose we start with primitive, meaningful elements and see if step by step we can build these elements up into something that corresponds to the system of real numbers.

As our primitive elements we can take the positive integers. They are a concrete aspect of the universe, in the form of the number of fingers on the human hand or whatever one chooses to count. As the 19^th century German mathematician Leopold Kronecker put it, the positive integers are the work of God and all the other types of number are the work of man. In the late 19^th century Giuseppe Peano of Italy provided a primitive description of the positive integers in terms of five axioms: (1) 1 is a positive integer; (2) every positive integer has a unique positive integer as its successor; (3) no positive integer has 1 as its successor; (4) distinct positive integers have distinct successors; (5) if a statement holds for the positive integer 1, and if, whenever it holds for a positive integer, it also holds for that integer’s successor, then the statement holds for all positive integers. (This last axiom is the famous “principle of mathematical induction”).

Now comes the fiat lux (“Let there be light”) of the whole business. Axiom: There exists a Peano system. This stroke creates the positive integers because the Peano system, or system of objects that fulfills the five requirements, is essentially equivalent to the set of positive integers. From Peano’s five rules all the familiar features of the positive integers can be deduced.

Once we have the positive integers at our disposal to work with and to mold, we can go merrily on our way, as Kronecker suggested, and construct extensions of the number idea. By operations with the positive integers, for example, we can create the negative integers and zero. A convenient way to do this is by operating with pairs of positive integers. Think of a general pair denoted (a, b) from which we shall create an integer by the operation a-b. When a is greater than b, the subtraction a-b produces a positive integer; when a is equal to b, then a-b produces zero. Thus pairs of positive integers can represent all the integers – positive, negative and zero. It is true that a certain ambiguity arises from the fact that a given integer can be represented by many different pairs; for instance, the pair (6, 2) stands for 4, but so do (7, 3), (8, 4) and a host of other possible combinations. We can reduce the ambiguity to unimportance, however, simply by agreeing to consider all such pairs as being identical.

Using only positive integers, we can write a rule that will determine when one pair is equal to another. The rule is that (a, b)=(c, d) if and only if a+d=b+c. (Note that the latter equation is a rephrasing of a-b=c-d, but it does not involve any negative integers, whereas the subtraction terms may.) It can easily be shown that this rule for deciding the equality of pairs of integers satisfies the three arithmetical laws governing equality, namely (1) the reflexive law: (a, b)=(a, b); (2) the symmetric law: if (a, b)=(b, c), then (b, c)=(a, b); (3) the transitive law: if (a, b)=(c, d) and (c, d)=(e, f), then (a, b)=(e, f).

We can now proceed to introduce conventions defining the addition and the multiplication of pairs of positive integers, again using only positive terms. For addition we have (a, b)+(c, d)=(a+c, b+d). Since (a, b) represents a-b and (c, d) represents c-d, the addition here is (a-b)+(c-d). Algebraically this is the same as (a+c)-(b+d), and that is represented by the pair (a+c, b+d) on the right side of the equation. Similarly, the multiplication of pairs of positive integers is defined by the formula (a, b)•(c, d)=(ac+bd, ad+bc). Here (a, b)(c, d) or (a-b)(c-d) can be expressed algebraically as (ac+bd)-(ad+bc), and this is represented on the right side of the equation by the pair (ac+bd, ad+bc).

It can be shown in detail that all the familiar operations with integers (positive, negative and zero), when performed with such pairs of positive integers, will produce the same results.

Having constructed all the integers (as pairs of positive integers), we can go on to create all the other real numbers and even the complex numbers. The rational numbers, or fractions, which are pairs of integers in the ordinary system, can be represented as pairs of pairs of positive integers. For the real numbers, made up of infinite sequences of integers, we must set up infinite sequences of rationals rather than pairs. When we come to the complex numbers, we can again use pairs; indeed, it was for these numbers that the device of number pairs was first employed (by Hamilton). We can think of a complex number, a+b 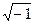, as essentially a pair of real numbers (a, b) with the first number of the pair representing the real element and the second representing the imaginary element of the complex number. Now, pairs will be considered equal only if they contain the same numbers in the same order; that is, (a, b)=(c, d) only if a=c and b=d. The rule for addition will be the same as in the case of the real numbers: (a, b)+(c, d)=(a+c, b+d). This parallels the “ordinary” outcome of the addition of two complex numbers: (a+b 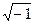)+ (c+d 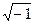)=(a+c)+(b+d) 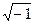. The multiplication formula for complex numbers, (a, b)•(c, d)=(ac-bd, ad+bc), also corresponds to the ordinary multiplication of such numbers: (a+b 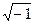) (c+d 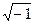)=(ac-bd)+(ad+bc) 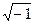. Pairs of real numbers manipulated according to these rules reproduce all the familiar behavior of the complex numbers. And the mysterious 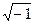, that “amphibian between being and not being”, emerges from the sea of axiomatics as the number pair (0, 1).

Thus, by four steps of construction and abstraction, we have advanced from the primitive positive integers to the complex numbers. Pairs of positive integers, combined in a certain way, lead to the set of all the integers. Pairs of integers (that is to say now, pairs of pairs of positive integers), combined in a different way, lead to the rational numbers. Infinite sequences of rational numbers lead to real numbers. Finally, pairs of real numbers lead to the complex numbers.

Looking back over the 2500 years that separate us from Pythagoras, we can make our two streams of thinking about numbers. There is the stream of synthesis, which began with tally marks and went on to build up number concepts of increasing complexity, un much the same way that a complex molecule is built up from atoms. On the other hand, there is a stream of analysis whereby mathematicians have sought to arrive at the essence of numbers by breaking down the complexities to their most primitive elements. Both streams are of enormous importance. Professional mathematicians today tend to play down number as such, favoring the qualitative aspects of their science and emphasizing the logical structure and symbolic potentialities of mathematics.

Modern number theories are now diffusing rapidly throughout our educational system, even down to the elementary schools. There are programs for teaching advanced number concepts, from set theory to matrices, to students in high school. It seems safe to say that the coming generation will be imbued with an unprecedented interest in the fascinating uses and mysteries of numbers.

***