
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВПЦ “Київський університет”, 2006 4 страница
|
|
Підставляння їх у рівняння теплопровідності дає
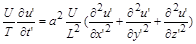 .
.
Два степеневі комплекси масштабів визначальних змінних явища теплопровідності
 і
і 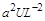 ,
,
один з яких містить у своєму складі коефіцієнт температуропровідності середовища 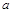 , зводяться до безрозмірного вигляду діленням одержаного рівняння на степеневий комплекс
, зводяться до безрозмірного вигляду діленням одержаного рівняння на степеневий комплекс  . Рівняння теплопровідності при цьому набуває такого вигляду:
. Рівняння теплопровідності при цьому набуває такого вигляду:
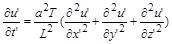 .
.
Єдиний безрозмірний степеневий комплекс 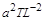 , який залишився в рівнянні, є критерієм подібності явища теплопровідності. Він має історичну назву – критерій подібності Фур’є:
, який залишився в рівнянні, є критерієм подібності явища теплопровідності. Він має історичну назву – критерій подібності Фур’є:
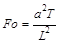 .
.
3.2. ТЕОРЕМИ ПОДІБНОСТІ
Основні положення теорії подібності зазвичай систематизуються у вигляді першої, другої та третьої теорем подібності; перші дві визначають необхідні, а третя – необхідні й достатні умови подібності.
Перша теорема подібності. В основному сучасному формулюванні, яке враховує можливість існування різних типів подібності, перша теорема має такий вигляд: явища, які є подібними в тому чи іншому розумінні (повно, наближено, фізично, математично тощо), мають певні комбінації параметрів, які називаються критеріями подібності, і які є чисельно однаковими для подібних явищ.
Отже, перша теорема подібності стверджує, що для явищ (об’єктів, процесів), які є подібними в тому чи іншому розумінні, існують однакові за формою алгебраїчного запису й рівні чисельно безрозмірні степеневі комплекси (добутки та частки) певних груп фізичних величин, які характеризують ці явища. Ця теорема формулює необхідну умову існування подібності (однакові критерії подібності в подібних явищах), але вона не вказує способів установлення подібності й способу її реалізації при побудові моделей.
У справедливості тверджень першої теореми ми переконались на конкретному прикладі, розглядаючи подібні явища теплопровідності.
Перша теорема подібності називається також теоремою Ньютона або Ньютона – Бертрана.
Друга теорема подібності. В основному формулюванні ця теорема має такий вигляд: будь-яке повне рівняння фізичного процесу, яке записане в певній системі одиниць, може бути зображеним функціональною залежністю між критеріями подібності, які формуються з параметрів, що характеризують процес.
Ця теорема часто називається 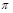 -теоремою, оскільки критерії подібності, які характеризують подібні процеси, найчастіше позначають грецькою літерою
-теоремою, оскільки критерії подібності, які характеризують подібні процеси, найчастіше позначають грецькою літерою 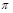 .
.
Друга теорема подібності встановлює можливість зображення інтеграла диференціального рівняння фізичного процесу не як функції параметрів процесу й системи, у якій відбуваються ці процеси, а як функції відповідно побудованих деяких безрозмірних величин – критеріїв подібності. Якщо диференціальне рівняння, яке характеризує процес, проінтегровано, то одержаний інтеграл дозволяє отримати однозначний функціональний зв’язок між критеріями подібності відповідно до тих припущень, які були прийняті при складанні та інтегруванні даного рівняння. Якщо ж диференціальне рівняння відсутнє або не інтегрувалось, то тип функціональних зв’язків між критеріями подібності не буде встановлений.
Друга теорема базується на дослідженнях Букінгема, Федермана та Еренферст-Афанасьєвої. Можливість зображення інтеграла як функції від критеріїв подібності, знайдених з диференціального рівняння, була строго доведена для частинного випадку Букінгемом. У більш загальному вигляді це положення як математична теорема було доведено Федерманом. Еренферст-Афанасьєва навела доведення в загальному вигляді і знайшла умови, за яких інтеграл можна зобразити як функцію критеріїв подібності.
Проілюструємо справедливість тверджень другої теореми подібності на конкретному прикладі.
Розглядається процес зміни в часі  напруги
напруги 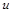 на конденсаторі в контурі, який утворено послідовним з’єднанням конденсатора ємністю
на конденсаторі в контурі, який утворено послідовним з’єднанням конденсатора ємністю 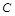 з активним елементом, що має опір
з активним елементом, що має опір 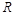 . Початком процесу є вмикання такого електричного контуру на сталу напругу
. Початком процесу є вмикання такого електричного контуру на сталу напругу 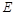 (рис. 1.3.1).
(рис. 1.3.1).
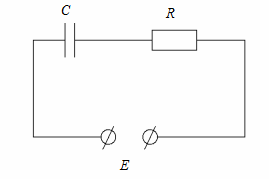
Рис. 1.3.1
За різних значень C, R, E процеси в електричному контурі, що розглядається, явно матимуть якісно однаковий характер, що дозволяє розглядати їх як групу подібних процесів.
Перехідний процес у такому контурі при вмиканні сталої напруги Е описується лінійним диференціальним рівнянням
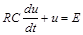 . (1.3.5)
. (1.3.5)
Розв’яжемо це рівняння. Спочатку розв’яжемо відповідне однорідне рівняння
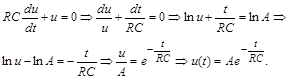
За методом варіації довільної сталої шукатимемо розв’язок рівняння (1.3.5) у вигляді
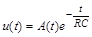 , (1.3.6)
, (1.3.6)
де 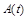 – поки що невідома функція.
– поки що невідома функція.
Підставимо (1.3.6) у (1.3.5):
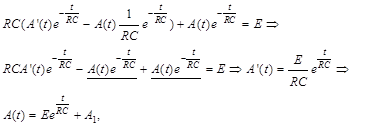 (1.3.7)
(1.3.7)
де 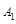 – довільна стала. Підстановка (1.3.7) у (1.3.6) дозволяє отримати загальний розв’язок рівняння (1.3.5) у вигляді
– довільна стала. Підстановка (1.3.7) у (1.3.6) дозволяє отримати загальний розв’язок рівняння (1.3.5) у вигляді
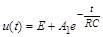 .
.
З нульової початкової умови 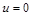 при
при  матимемо
матимемо 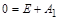 при
при  . Звідси
. Звідси 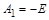 , і розв’язок рівняння (1.3.5) за нульової початкової умови набуде вигляду
, і розв’язок рівняння (1.3.5) за нульової початкової умови набуде вигляду
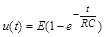 . (1.3.8)
. (1.3.8)
Усі члени будь-якого рівняння, яке описує який-небудь фізичний процес, завжди мають однакову розмірність (правило Фур’є), тому рівняння (1.3.5) можна привести до безрозмірного вигляду, тобто зобразити його у вигляді суми безрозмірних членів, якщо поділити його на один із членів, наприклад на 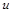 :
:
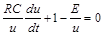
або, позначаючи
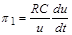 і
і  ,
,
матимемо
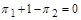 . (1.3.9)
. (1.3.9)
Перетворимо 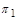 , скориставшись правилом заміщення.
, скориставшись правилом заміщення.
Правило заміщення. Якщо
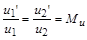 , (1.3.10)
, (1.3.10)
де 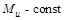 , то
, то
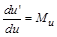 . (1.3.11)
. (1.3.11)
Щоб переконатися у справедливості цього правила, зазначимо, що пропорції
 і
і 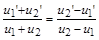
еквівалентні згідно з властивостями пропорцій. Тому врахування (1.3.10) дає
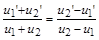
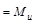 ,
,
звідки
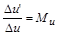 , (1.3.12)
, (1.3.12)
де  ,
, 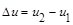 .
.
Перейдемо до границі при 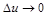 в обох частинах рівності (1.3.12)
в обох частинах рівності (1.3.12)  .
.
Ураховуючи, що 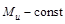 , отримаємо (1.3.11).
, отримаємо (1.3.11).
Звідси маємо правило: вивчаючи подібність, замість похідної від характерної величини можна розглядати відношення відповідних величин – так званий інтегральний аналог. Аналогічно й для старших похідних.
Тому при вивченні подібних процесів в електричному контурі замість похідної 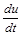 можна розглядати її інтегральний аналог
можна розглядати її інтегральний аналог 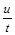 , звідси
, звідси
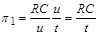 .
.
Отже, 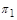 і
і 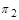 у рівнянні (1.3.9) можна зобразити у вигляді
у рівнянні (1.3.9) можна зобразити у вигляді
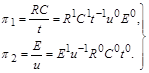 (1.3.13)
(1.3.13)
Вирази для 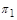 і
і 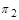 , що мають вигляд безрозмірних степеневих комплексів параметрів, які характеризують процес, що розглядається, називаються критеріями подібності; критерії подібності чисельно однакові для відповідних точок подібних процесів.
, що мають вигляд безрозмірних степеневих комплексів параметрів, які характеризують процес, що розглядається, називаються критеріями подібності; критерії подібності чисельно однакові для відповідних точок подібних процесів.
Спосіб установлення критеріїв подібностіза відомим математичним описанням процесу шляхом приведення його до безрозмірного вигляду, при якому символи диференціювання та інтегрування у виразах для критеріїв подібності опускаються, називається правилом інтегральних аналогів.
Наявність критеріїв подібності 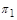 і
і 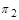 у задачі, що розглядається, дозволяє розв’язок цієї задачі зобразити як функцію критеріїв подібності
у задачі, що розглядається, дозволяє розв’язок цієї задачі зобразити як функцію критеріїв подібності
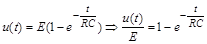 ,
,
звідки
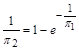 або
або 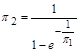 . (1.3.14)
. (1.3.14)
Приклад, який ми розглянули, підтверджує положення першої теореми подібності: явища, що є подібними, мають певні комбінації параметрів, які називаються критеріями подібності і є чисельно однаковими для подібних явищ.
Розглянутий приклад ілюструє також другу теорему подібності. А саме: одержання співвідношень (1.3.9) і (1.3.13) підтверджує положення другої теореми подібності, що будь-яке повне рівняння фізичного процесу може бути зображеним функціональною залежністю між критеріями подібності (у прикладі – співвідношення (1.3.9)), які формуються з параметрів, що характеризують процес (у прикладі – співвідношення (1.3.13)).
Розглянутий приклад підтверджує також той факт, що друга теорема подібності встановлює можливість зображення інтеграла диференціального рівняння фізичного процесу не як функцію параметрів процесу і системи, у якій відбуваються ці процеси (у прикладі – функція (1.3.8), яка встановлює зв’язок між 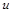 і
і 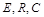 і
і  ), а як функцію критеріїв подібності (у прикладі – співвідношення (1.3.14)). Така можливість була забезпечена тим, що диференціальне рівняння (1.3.5) математичної моделі процесу було проінтегровано. Якби цього не вдалося зробити (напр., через складність рівняння), то теоретичний аналіз, що був застосований у прикладі, не дозволив би знайти зв’язок між критеріями подібності.
), а як функцію критеріїв подібності (у прикладі – співвідношення (1.3.14)). Така можливість була забезпечена тим, що диференціальне рівняння (1.3.5) математичної моделі процесу було проінтегровано. Якби цього не вдалося зробити (напр., через складність рівняння), то теоретичний аналіз, що був застосований у прикладі, не дозволив би знайти зв’язок між критеріями подібності.
Слід зауважити (і це дуже важливо!), що критерії подібності подібних процесів можна отримати й у тому випадку, коли математичне описання процесу є невідомим. Для знаходження критеріїв подібності в такому разі застосовується метод аналізу розмірностей фізичнихвеличин, які визначають характер процесу, що розглядається. До цього методу ми звернемося пізніше.
Третя теорема подібності. У найбільш поширеному формулюванні третя теорема має такий вигляд: необхідними й достатніми умовами для подібності явищ, які зіставляються між собою, є пропорційність відповідних параметрів, що входять в умови однозначності математичних моделей цих явищ, а також рівність критеріїв подібності цих явищ.
Третя теорема подібності називається також оберненою теоремою подібності або теоремою Кірпічова – Гухмана.
До умов однозначності, які згадуються в теоремі, належать такі, незалежні від механізму самого явища, фактори й умови:
· геометричні властивості системи, у якій відбувається процес;
· фізичні параметри середовища й тіл, які утворюють систему;
· початковий стан системи (початкові умови);
· умови на межах системи (межові або крайові);
· взаємодія об’єкта й зовнішнього середовища.
Розглянутий нами приклад про електричне коло підтверджує положення третьої теореми подібності, а саме: розглядаючи подібні процеси з пропорційними величинами 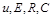 у відповідні моменти часу
у відповідні моменти часу  , ми прийшли до критеріїв подібності подібних процесів (у прикладі – співвідношення (1.3.13)), які чисельно однакові для подібних процесів у відповідні моменти часу.
, ми прийшли до критеріїв подібності подібних процесів (у прикладі – співвідношення (1.3.13)), які чисельно однакові для подібних процесів у відповідні моменти часу.
Установлення критеріїв подібності означає перехід від величин, що характеризують процес (у прикладі – 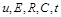 ), до безрозмірних величин (у прикладі –
), до безрозмірних величин (у прикладі – 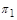 і
і 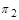 ), які називаються критеріями подібності і дають можливість змінити характер аналізу процесу, що відбувається в системі. Критерії подібності стаютьновими змінними системи, їх називають узагальненими змінними системи.
), які називаються критеріями подібності і дають можливість змінити характер аналізу процесу, що відбувається в системі. Критерії подібності стаютьновими змінними системи, їх називають узагальненими змінними системи.
Існує думка, що тільки друга теорема подібності може розглядатися як теорема в тому розумінні, у якому це поняття використовується в математиці, а перша й третя теореми подібності є правилами виявлення й забезпечення подібності. У даному курсі лекцій використовується найбільш поширена термінологія – назва першої теореми, яку ввів ще Ньютон, і запропонована Кірпічовим і Гухманом назва третьої теореми.
4. МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ
ЗА ВІДСУТНОСТІ МОДЕЛЬНОГО
ДИФЕРЕНЦІАЛЬНОГО РІВНЯННЯ
Якщо об’єкт, що вивчається, складний, то часто важко описати його за допомогою математичної моделі, тобто складаючи відповідне визначальне рівняння для основної величини, яка характеризує об’єкт. Відсутність математичного описання оригіналу, а отже й відсутність математичного описання моделі, робить неможливим установлення масштабів і критеріїв подібності за допомогою відповідних визначальних рівнянь оригіналу й моделі.
У багатьох випадках це вдається зробити, використовуючи аналіз розмірностей усіх фізичних величин, які визначають стан матеріального об’єкта, що вивчається, а також 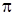 -теорему, яка вказує метод установлення критеріїв подібності, коли математичні описання оригіналу й моделі невідомі.
-теорему, яка вказує метод установлення критеріїв подібності, коли математичні описання оригіналу й моделі невідомі.
Аналіз розмірностей і 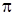 - теорема виявляються також дуже корисними при створенні розрахункових математичних моделей на основі даних, які отримуються шляхом натурних експериментів.
- теорема виявляються також дуже корисними при створенні розрахункових математичних моделей на основі даних, які отримуються шляхом натурних експериментів.
4.1. РОЗМІРНОСТІ
Наріжним каменем теорії розмірностей є твердження: основою будь-якої точної науки є вимірювання величин.
Вимірювання – це порівняння шляхом експерименту даної величини з деяким її значенням, прийнятим за одиницю виміру.
Нехай 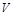 – величина, яка вимірюється, а
– величина, яка вимірюється, а 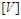 – її одиниця виміру. Виміряти
– її одиниця виміру. Виміряти 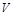 – це означає знайти число, що виражає відношення величини, яка вимірюється, до одиниці виміру, тобто
– це означає знайти число, що виражає відношення величини, яка вимірюється, до одиниці виміру, тобто
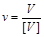 ;
;
це число називається числовим значенням величини, яка вимірюється. Таким чином, числове значення величини, яка вимірюється, обернено пропорційне до величини одиниці виміру.
Одиниці виміру різних фізичних величин у принципі можна вибирати як завгодно й незалежно одна від одної. Проте, довільно вибираються одиниці виміру небагатьох фізичних величин.
Різні фізичні величини можуть бути пов’язані між собою певними співвідношеннями. Тому, якщо вибрати довільно одиниці виміру деяких з них, то через ці одиниці можна визначити одиниці виміру всіх інших фізичних величин.
Фізичні величини, розмір одиниць виміру яких вибирається довільно, називаються основними фізичними величинами. Одиниці виміру основних фізичних величин називаються основними одиницями виміру.
Одиниці всіх інших вторинних фізичних величин виражаються через основні за допомогою відповідних законів і рівнянь зв’язку. Одиниці виміру вторинних фізичних величин називаються похідними одиницями виміру.
Сукупність основних і похідних одиниць виміру складає системуодиниць виміру.
У міжнародній системі одиниць, яка скорочено називається SI, основними фізичними величинами є довжина, маса, час, сила електричного струму, термодинамічна температура, сила світла.
Основними одиницями вимірув цій системі вибрано метр, кілограм, секунду, ампер, кельвін і канделу. Додатковими одиницями вимірує радіан – одиниця плоского кута і стерадіан – одиниця тілесного кута.
Припустимо, що між фізичною величиною 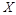 , для якої знаходиться похідна одиниця виміру
, для якої знаходиться похідна одиниця виміру 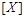 , і фізичними величинами
, і фізичними величинами 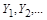 , для яких установлено незалежні основні одиниці виміру
, для яких установлено незалежні основні одиниці виміру 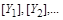 , існує залежність
, існує залежність
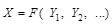 . (1.4.1)
. (1.4.1)
Такою ж має бути й залежність між числовими значеннями 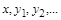 цих фізичних величин:
цих фізичних величин:
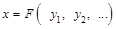 . (1.4.2)
. (1.4.2)
Оскільки
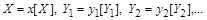 ,
,
то згідно з рівністю (1.4.1), матимемо
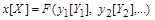 , (1.4.3)
, (1.4.3)
звідки випливає, що 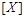 є деякою функцією від
є деякою функцією від 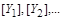 ,
,
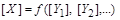 , (1.4.4)
, (1.4.4)
яка потребує визначення. З рівностей (1.4.2)–(1.4.4) матимемо
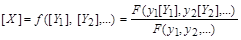 . (1.4.5)
. (1.4.5)
Частка від ділення чисельника цього дробу на знаменник не буде залежати від 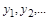 тільки за умови, що функція
тільки за умови, що функція 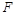 однорідна, тобто має вигляд степеневого комплексу
однорідна, тобто має вигляд степеневого комплексу
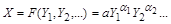 , (1.4.6)
, (1.4.6)
де 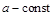 . Тоді згідно з (1.4.5)
. Тоді згідно з (1.4.5)
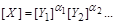 . (1.4.7)
. (1.4.7)
Таким чином, для знаходження похідних одиниць виміру придатними є тільки такі закономірності, які виражаються однорідними функціями.
Формула (1.4.7), що показує, як похідна одиниця виміру залежить від основних одиниць, називається формулою розмірності відповідної фізичної величини.
Символічний (буквений) вираз залежності похідної одиниці виміру деякої фізичної величини від основних одиниць у вигляді степеневого комплексу називається розмірністю цієї фізичної величини.
Квадратними дужками будемо позначати розмірність величини: позначення 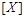 означатиме розмірність величини
означатиме розмірність величини 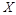 . Розмірність виражається в символах основних одиниць виміру.
. Розмірність виражається в символах основних одиниць виміру.
Наведемо розмірності й символи основних одиниць системи СІ:
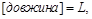 одиниця виміру – метр (м);
одиниця виміру – метр (м);
 одиниця виміру – кілограм (кг);
одиниця виміру – кілограм (кг);
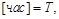 одиниця виміру – секунда (с);
одиниця виміру – секунда (с);
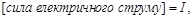 одиниця виміру – ампер (А);
одиниця виміру – ампер (А);
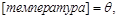 одиниця виміру – кельвін (К);
одиниця виміру – кельвін (К);
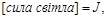 одиниця виміру – кандела (кд).
одиниця виміру – кандела (кд).
Згідно з формулою (1.4.7) розмірність фізичної величини 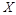 у системі СІ в загальному випадку матиме вигляд
у системі СІ в загальному випадку матиме вигляд
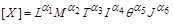 . (1.4.8)
. (1.4.8)
На практиці, говорячи про розмірності різних величин, часто мають на увазі просто одиниці, у яких виражаються числові значення цих величин. При цьому замість рівності (1.4.8) пишуть
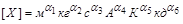 . (1.4.9)
. (1.4.9)
Приклад 1. Частота періодичного процесу з періодом 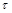 дорівнює
дорівнює 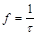 . Одиницею виміру частоти служить герц – частота періодичного процесу, у якому один цикл відбувається за одну секунду. Якщо
. Одиницею виміру частоти служить герц – частота періодичного процесу, у якому один цикл відбувається за одну секунду. Якщо 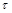 вимірюється в секундах (с), то частота
вимірюється в секундах (с), то частота 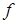 виражається в герцах (Гц). Формула розмірності частоти
виражається в герцах (Гц). Формула розмірності частоти
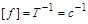 .
.
Однак часто пишуть 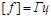 .
.
Крім розмірних величин у фізичних задачах зустрічаються так звані безрозмірні.
Величина 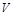 називається безрозмірною, якщо її формула розмірності має вигляд
називається безрозмірною, якщо її формула розмірності має вигляд
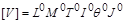 ,
,
при цьому
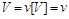 .
.
На цій підставі, маючи справу з безрозмірною величиною, говорять про нульову розмірність або розмірність, якадорівнює одиниці.
Оскільки формула розмірності (1.4.8) може бути написаною для будь-якої величини, а кожна величина має відповідну розмірність, то такі величини слід називати величинами з одиничною розмірністю 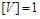 .
.
Прикладами таких величин є відношення фізично однорідних величин: відносна зміна будь-якої величини
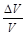 ,
,
відношення дуги кола до радіуса тощо. Безрозмірними величинами є абстрактні змінні й сталі, з якими має справу “чиста” математика.
Функціональна залежність (1.4.6), яка вибрана для встановлення похідної одиниці виміру 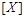 величини
величини 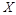 , називається визначальним рівнянням цієї величини.
, називається визначальним рівнянням цієї величини.
Коефіцієнт пропорційності 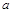 у такому рівнянні в загальному випадку залежить від вибору одиниць виміру відповідних величин. У визначальному рівнянністалий коефіцієнт
у такому рівнянні в загальному випадку залежить від вибору одиниць виміру відповідних величин. У визначальному рівнянністалий коефіцієнт 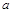 завжди є безрозмірною величиною
завжди є безрозмірною величиною
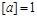 ,
,
причому в системі СІ його числове значення дорівнює одиниці 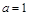 . Тому в системі СІ формула розмірності (1.4.7) повністю копіює визначальне рівняння (1.4.6).
. Тому в системі СІ формула розмірності (1.4.7) повністю копіює визначальне рівняння (1.4.6).
Якщо ж залежність (1.4.6) не є визначальною, то коефіцієнт 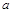 , який не дорівнює одиниці, може бутиякбезрозмірною, так і розмірноювеличиною. У першому випадку формула розмірності (1.4.7) копіює рівняння (1.4.6) з точністю до сталого безрозмірного множника, у другому – замість рівності (1.4.7) маємо
, який не дорівнює одиниці, може бутиякбезрозмірною, так і розмірноювеличиною. У першому випадку формула розмірності (1.4.7) копіює рівняння (1.4.6) з точністю до сталого безрозмірного множника, у другому – замість рівності (1.4.7) маємо
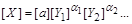 (1.4.10)
(1.4.10)
Приклад 2. Кінетична енергія тіла масою 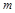 , яке рухається зі швидкістю
, яке рухається зі швидкістю 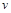 , дорівнює
, дорівнює  .
.
Оскільки швидкість 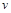 дорівнює шляху
дорівнює шляху 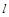 , поділеному на час
, поділеному на час  , тобто
, тобто 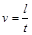 , то остаточно буде
, то остаточно буде
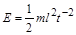 .
.
Це рівняння має вигляд рівності (1.4.7), але в системі СІ воно не є визначальним для енергії. Енергія, тобто працездатність, має розмірність роботи 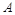 , тобто
, тобто 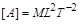 . У системі СІ коефіцієнт
. У системі СІ коефіцієнт 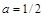 – безрозмірна величина, і у формулі розмірності
– безрозмірна величина, і у формулі розмірності
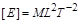
його немає.
Приклад 3. Одиниця виміру сили в системі СІ може бути встановленою на основі другого закону Ньютона (сила 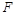 пропорційна масі
пропорційна масі 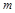 і прискоренню
і прискоренню 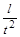 ):
):
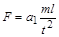 ,
,
а також закону всесвітнього тяжіння (сила 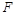 пропорційна добутку мас
пропорційна добутку мас 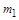 і
і 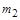 і обернено пропорційна квадрату відстані
і обернено пропорційна квадрату відстані  )
)