ВПЦ “Київський університет”, 2006 8 страница

.

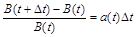Припускаючи диференційовність функції B (t), з останньої рівності граничним переходом при 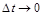отримаємо 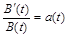, звідки

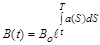. (2.2.10)

Формула (2.2.10) виражає вартість облігації в момент t і є неперервним аналогом формули складних відсотків.

Акція – це документ про підтвердження права на частину майна підприємства та на певну частину прибутку. Ціна акції залежить від того, настільки прибутковим є підприємство, і від інших чинників (загальна політична ситуація в країні, економічний спад чи піднесення). Тобто на ціну впливають мікроекономічні фактори, що мають випадковий характер, і макроекономічні (загальнодержавні чинники), які на певний період часу можна вважати невипадковими. Тому ціна акції в момент t – S(t) є випадковою.

Отримаємо рівняння для визначення ціни акції, припустивши, що в математичній моделі фінансового ринку випадкові чинники є незалежними та їх кількість є великою. Тобто результуючий випадковий фактор є сумою великої кількості однаково розподілених незалежних випадкових величин, що дає змогу застосувати в моделі центральну граничну теорему. При цьому зручніше розглядати не абсолютну зміну вартості акцій 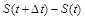, а відносну: 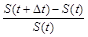. Наприклад, якщо акція вартістю 1 грн дешевшає на 1 к., то акція вартістю 100 грн дешевшає на 1 грн. Тому відносна зміна вартості є зручнішою. Отже, замість 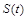розглянемо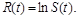

Нехай спочатку час 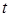приймає дискретну послідовність значень 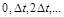Якщо немає глобальних фінансових змін, політична ситуація стабільна, то 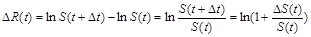є випадковою величиною з нульовим математичним сподіванням, оскільки за припущенням моделі всі випадкові фактори однаково можливі, тому в середньому зміна ціни не відбувається. При цьому дисперсія 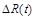пропорційна 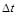, тобто 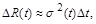де 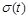– коефіцієнт зміни, його називають коефіцієнтом дифузії або коефіцієнтом волатильності. Дійсно,

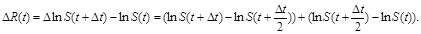
Згідно з моделлю, ці прирости незалежні, а тому дисперсії додаються. Отже, дисперсі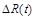я для 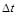удвічі більша, ніж дисперсія для 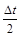; те ж саме виконується для 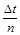і т. д. Звідси випливає лінійність зміни. Тому, оскільки 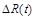є сумою однаково розподілених, незалежних випадкових величин з нульовим математичним сподіванням і дисперсією, пропорційною довжині 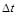, то згідно з центральною граничною теоремою 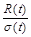має нормальний розподіл (при 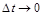) з нульовим математичним сподіванням, а отже, при 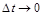є вінерівським процесом 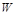(t), і

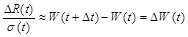при .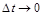

Маємо

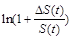
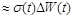. (2.2.11)

Оскільки при малих 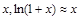, то формулу (2.2.11) можна переписати у вигляді

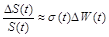. (2.2.12)

Вона стане точною, якщо в останній рівності перейти до границі при 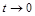і переписати її у вигляді

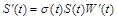(2.2.13)

або в диференціальній формі:

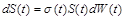, (2.2.14)

або в інтегральній:

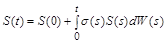. (2.2.15)

Однак у класичному сенсі ні похідної , ні 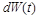, ні інтеграла у формулі (2.2.15) не існує, оскільки відомо, що траєкторії вінерівського процесу, які є неперервними функціями, ніде не диференційовані та мають необмежену варіацію, тому інтеграл у (2.2.15) не можна розглядати як звичайний інтеграл Стільт’єса. Інтеграл у (2.2.15) розуміється як спеціальний стохастичний інтеграл Іто, а диференціал у (2.2.14) – як стохастичний диференціал Іто, конструкцію якого можна знайти в будь-якому підручнику з випадкових процесів.

Формула (2.2.14) отримана за відсутності макроекономічних чинників. Якщо їх урахувати (напр., інфляцію), то зміна вартості акції буде сумарним результатом макроекономічних чинників, вплив яких можна вважати лінійним (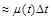), і мікроекономічних (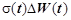). Тому остаточно отримаємо:

.

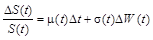Перейшовши до границі при 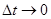, для вартості акцій 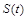можна написати лінійне стохастичне диференціальне рівняння

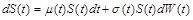, (2.2.16)

де перший диференціал звичайний, а другий – стохастичний.

Розв’язок цього рівняння [4] матиме вигляд

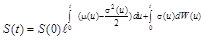. (2.2.17)

Якщо і 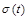– сталі, то формула (2.2.17) набуває вигляду

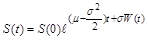(2.2.18)

і називається формулою Самуельсона. Вона дозволяє моделювати зміну вартості акцій за допомогою вінерівського процесу та знаходити ймовірносні характеристики 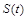(розподіли, моменти тощо).

Описана вище модель називається моделлю 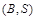-ринку (облігації, акції). Маючи формули для вартості акцій і облігацій, інвестор може вигідніше вкладати свої кошти в ті чи інші папери, тобто будувати свою стратегію поведінки на ринку цінних паперів, а відтак отримувати прибуток від гри на біржі чи, принаймні, застрахувати себе від збитків.

3. НЕЛІНІЙНІ МОДЕЛІ ТЕПЛОПРОВІДНОСТІ
ТА ФІЛЬТРАЦІЇ

3.1. РОЗПОВСЮДЖЕННЯ ТЕПЛА
ПРИ ТЕПЛОПРОВІДНОСТІ,
ЩО ЗАЛЕЖИТЬ ВІД ТЕМПЕРАТУРИ

Класична лінійна теорія розповсюдження тепла в середовищі зі сталими теплопровідністю та теплоємністю вважається найбільш вивченим розділом математичної фізики, чого не можна сказати про нелінійні задачі розповсюдження тепла. Такі задачі виникають, коли в рівнянні розповсюдження тепла розглядаються джерела тепла, потужність яких залежить від температури. З такими задачами ми зустрічаємося в теорії розповсюдження полум’я, у теорії зірок. В обох випадках, разом із впливом температури на швидкість виділення тепла, має місце істотна залежність (як правило, степенева) теплопровідності й теплоємності від температури. Зараз у теорії горіння й теорії зірок добре вивчені одновимірні стаціонарні та квазі-стаціонарні процеси, у яких температура залежить тільки від однієї просторової змінної, що дає можливість переходити до звичайних диференціальних рівнянь. В ієрархії складності наступними є одновимірні нестаціонарні процеси, у яких температура залежить від однієї просторової змінної та часу. Відповідна до них математична модель є одномірним нелінійним рівнянням теплопровідності.

Загальне рівняння теплопровідності в інертному середовищі (без джерел тепла) має вигляд

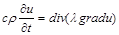. (2.3.1)

Якщо теплоємність 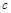пропорційна 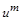, а теплопровідність 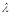пропорційна 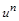, то (2.3.1) записується у вигляді

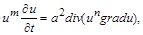(2.3.2)

де 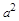– стала, що об’єднує коефіцієнти пропорційності й густину середовища при 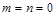, 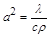. При перетворенні Кірхгофа

,

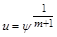
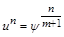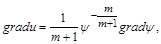
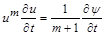
рівняння (2.3.2) набуває вигляду

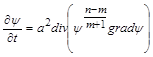, (2.3.3)

тобто стає рівнянням теплопровідності для випадку сталої теплоємності та степеневої залежності теплопровідності від температури. Тому досить обмежитися розглядом рівняння

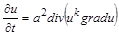. (2.3.4)

Розглянемо одновимірні нелінійні рівняння, коли від операторів 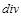та 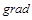залишаються тільки їх радіальні частини в циліндричній і сферичній системах координат:

.

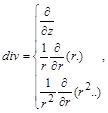
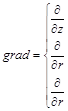Якщо ввести показник розмірності простору 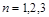, то наведені рівняння об’єднуються в рівняння вигляду

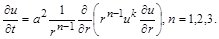(2.3.5)

Сім’ї розв’язків цього рівняння будемо шукати у вигляді добутку двох функцій, кожна з яких залежить тільки від одного аргументу [1]:

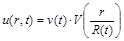. (2.3.6)

Змінна 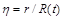називається змінною подібності тому, що значення функції 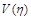дорівнює одній і тій самій сталій 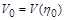для всіх точок кривої 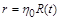на площині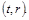

Виберемо розв’язок у вигляді (2.3.6) і відокремимо змінні в рівнянні

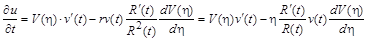
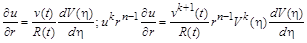
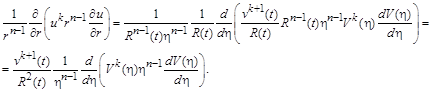
Згідно з цими виразами, рівняння (2.3.5) після домноження на 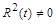переписується у вигляді

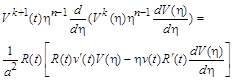. (2.3.7)

Ми не накладали обмежень на функції 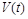та , крім умови 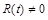. Для відокремлення змінних у рівнянні (2.3.7) припустимо, що

,

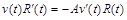де 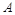– стала. Звідси 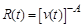або 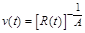. При цьому права частина рівняння (2.3.7) матиме вигляд

,

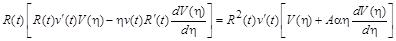що дозволяє зробити відокремлення змінних:

.

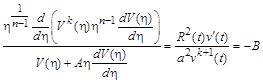Для визначення 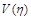, 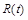і 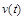одержимо звичайні диференціальні рівняння:

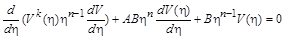. (2.3.8)

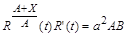. (2.3.9)

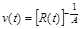. (2.3.10)

Загальний розв’язок рівняння (2.3.9) має вигляд

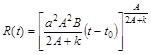. (2.3.11)

Тоді

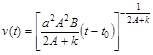. (2.3.12)

Домножимо рівняння (2.3.8) на 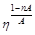і перепишемо його у вигляді

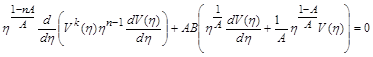
або

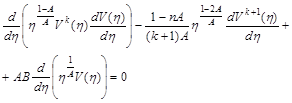. (2.3.13)

Якщ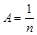о або 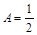, то рівняння (2.3.13) можна один раз проінтегрувати:

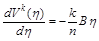. (2.3.14)

Інтегруючи (2.3.14) ще раз, отримаємо

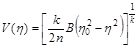(2.3.15)

– розв’язок, що залежить від довільної сталої 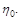При 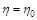він дорівнює нулю. З диференціального рівняння (2.3.7) випливає, що при 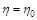дорівнює нулю перша й усі старші похідні. Тому для всіх 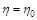функція 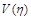тотожно дорівнює нулю. Отже,

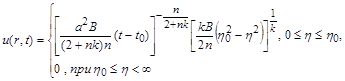(2.3.16)

, (2.3.17)

де 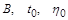– параметри.

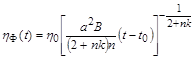– рівняння фронту розповсюдження, що відділяє збурене середовище від середовища, до якого в даний момент часу збурення ще не дійшло.

Швидкість розповсюдження збурення така:

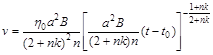. (2.3.18)

У лінійній теорії теплопровідності й дифузії поняття області впливу відсутнє: температура, концентрація й густина тільки асимптотично прямує до нуля на нескінченній відстані від джерела. У нелінійній теорії, якщо в початковому стані в середовищі теплопровідність дорівнює нулю, то в кожний даний момент часу теплове збурення охоплює тільки певний скінченний об’єм.

У другому частинному випадку 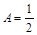маємо

.

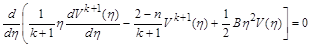Тоді .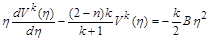

Звідси

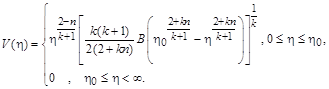(2.3.19)

Загальним розв’язком задачі буде

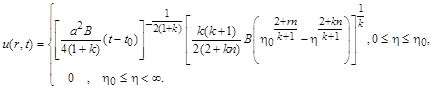
де 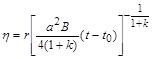залежить від параметрів .

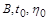Форма змінних подібності 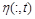залежить від параметрів 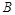і 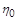. Вони можуть бути визначені за допомогою спеціальних крайових умов.

Особливий інтерес становлять процеси розповсюдження фіксованої кількості тепла, енергії або маси, виділених у початковий момент часу в початку координат.

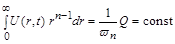. (2.3.20)

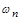– площа одиничної сфери в просторі 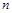змінних.

Підставляючи (2.3.6) у (2.3.20), отримуємо

.

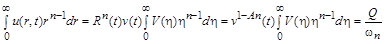Отже, .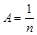

Такому значенню 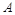відповідає розв’язок (2.3.16)–(2.3.17). Однак для фізики цікаві не всі такі розв’язки, а тільки ті, для яких 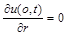, 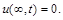Обидві умови виконуються автоматично, а використовується тільки одна:

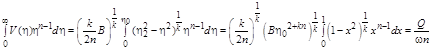
Звідси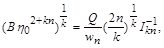

.

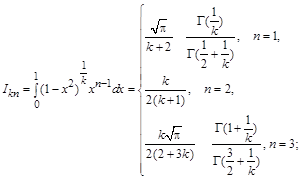
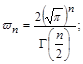
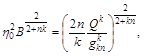
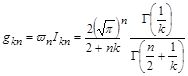Точні розв’язки залежать тільки від комбінації 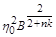параметрів 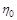та .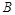

.

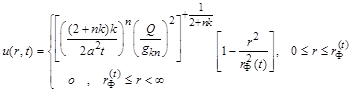
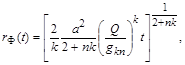
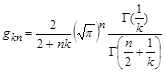3.2. РІВНЯННЯ ФІЛЬТРАЦІЇ

Під фільтрацією будемо розуміти рух, а точніше, просочування рідини або газу в пористому середовищі або середовищі з тріщинами.

Основними величинами, що визначають стан рідини чи газу в природному ґрунті, є густина 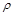, тиск 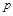і швидкість фільтрації. Характеристикою ґрунту або іншого середовища, у якому відбувається фільтрація, є пористість .

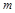Під швидкістю фільтрації 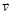розуміють витрати рідини чи газу, віднесені до одиниці площі, виділеної в пористому середовищі. Фільтрація – це рух частинок рідини через канали, що утворилися між частинками ґрунту або іншого пористого середовища.

Відношення загального об’єму каналів або пор, що знаходяться в деякому об’ємі пористого середовища, до всього об’єму цього середовища називається пористістю середовища .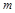

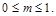
В основі теорії фільтрації лежить закон, установлений експериментально у 1852–1855 рр. французьким інженером А. Дарсі. Згідно з цим законом, кількість рідини чи газу пропорційна падінню гідродинамічного тиску в напрямку потоку рідини:

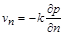, (2.3.21)

де 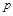– тиск, 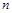– нормаль до одиничної площадки, а 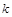– коефіцієнт фільтрації.

Якщо 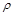– густина, то кількість рідини 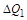, зібраної в деякому об’ємі 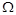за відрізок часу 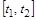, визначається інтегралом

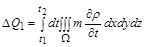. (2.3.22)

Кількість рідини 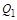у 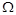, що відповідає заданій густині, визначається інтегралом

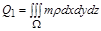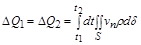, . (2.3.23)

Це співвідношення аналогічне відповідному співвідношенню, що визначає кількість накопиченого тілом тепла .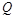

При виведенні рівняння фільтрації рідини або газу в пористому середовищі необхідно використати рівняння руху в’язкої рідини Нав’є – Стокса, а також рівняння нерозривності та стану. Їх використання обумовлене тим, що на відміну від теплопровідності й дифузії, процес фільтрації визначається густиною 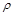, тиском 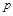і швидкістю фільтрації . Безпосереднє інтегрування рівнянь Нав’є – Стокса у випадку обтікання нескінченно великого числа частинок (при фільтрації) не можна виконати. Тому застосовують штучний підхід, що базується на використанні рівнянь руху Ейлера.

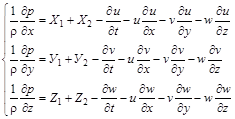, (2.3.24)

де 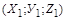– вектор масових сил, 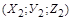– вектор сил опору, 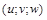– вектор швидкості.

Вважатимемо, що компонентами сил ваги є 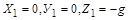, де 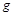– прискорення сили ваги. Знак “-” вибрано відповідно до вибору напрямку осі .

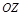Сили опору 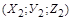, що виникають при обтіканні рідиною частинок пористого середовища, визначаються за допомогою закону Дарсі:

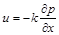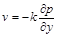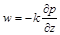, , . (2.3.25)

Для їх визначення в рівняннях (2.3.24) нехтують силами інерції та силою ваги. Це приводить до такого рівняння:

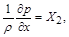
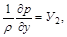
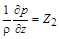. (2.3.26)

Використовуючи закон Дарсі, отримуємо

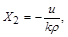
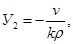
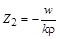. (2.3.27)

Якщо підставити в рівняння (2.3.24) знайдені компоненти сил, то отримуємо

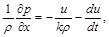
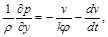(2.3.28)

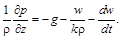
До цих рівнянь необхідно приєднати рівняння стану рідини чи газу (вони пов’язують густину 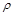і тиск )

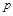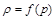(2.3.29)

і рівняння нерозривності

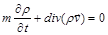. (2.3.30)

Однак така система рівнянь є невиправдано ускладненою. Як правило, сили інерції 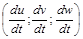досить малі, тому ними можна знехтувати в рівняннях (2.3.28). Тоді рівняння (2.3.28) спрощується:

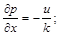
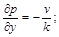
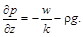(2.3.31)

Звідси випливають рівняння фільтрації:

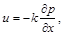
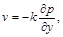
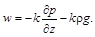(2.3.31 )

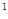Підставляючи знайдені 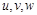у рівняння нерозривності й ураховуючи рівняння стану, отримаємо основне рівняння фільтрації відносно тиску :

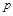. (2.3.32)

Фільтрація нестисливої рідини. Якщо рідина нестислива, то її густина – стала. Рівняння стану (2.3.29) у цьому випадку не використовується, а рівняння нерозривності набуває вигляду