
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВПЦ “Київський університет”, 2006 5 страница
|
|
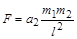 .
.
У системі СІ визначальним рівнянням для сили прийнято закон Ньютона. Одиниця виміру сили – ньютон (Н) визначається як сила, яка надає масі в 1 кгприскорення 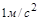 . Тому за формулою другого закону Ньютона
. Тому за формулою другого закону Ньютона
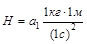
і, як наслідок, 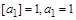 і
і
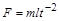 ,
,
а також
 .
.
У цьому випадку формула закону всесвітнього тяжіння визначає сталу 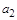 як гравітаційну сталу
як гравітаційну сталу
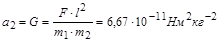 ,
,
яка має розмірність 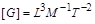 .
.
Висновки. Таким чином, формула розмірності похідної фізичної величини однозначно визначається вибором основних одиниць виміру й визначального рівняння.
Одна й та сама формула розмірності може відповідати різним фізичним величинам. Так, наприклад, у СІ розмірності [роботи], [енергії], [моменту сили], [кількості теплоти] збігаються й дорівнюють
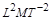 .
.
Кількість розмірних коефіцієнтів (фізичних сталих) у фізичних формулах залежить від кількості основних одиниць виміру. Чим більшою є кількість основних фізичних одиниць, тим більшою є кількість універсальних сталих у фізичних формулах. Це ускладнює формули й обчислення з їхньою допомогою. І навпаки, чим меншою є кількість основних одиниць виміру, тим меншою є кількість універсальних фізичних сталих і тим простішими є фізичні формули. Однак при цьому збільшується кількість похідних одиниць виміру, які мають однакові розмірності.
Переконаємося, що за допомогою формули розмірності (1.4.7)
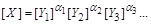
є можливим досить простий перехід від однієї системи одиниць до іншої.
Нехай для фізичних величин 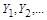 одиницями виміру в першій системіє
одиницями виміру в першій системіє 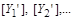 , а в другій –
, а в другій – 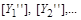 Відношення між одиницями виміру й відповідними числовими значеннями
Відношення між одиницями виміру й відповідними числовими значеннями 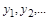 величин
величин 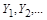 , які належать різним системам, визначають безрозмірні коефіцієнти
, які належать різним системам, визначають безрозмірні коефіцієнти
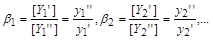 (1.4.11)
(1.4.11)
(оскільки  у першій і другій системах виміру, то
у першій і другій системах виміру, то
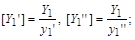
поділивши першу одержану рівність на другу, отримаємо 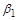 . Аналогічно отримуються інші безрозмірні коефіцієнти
. Аналогічно отримуються інші безрозмірні коефіцієнти 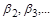 ). Безрозмірні коефіцієнти
). Безрозмірні коефіцієнти 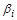 показують, у скільки разів одна одиниця виміру
показують, у скільки разів одна одиниця виміру 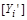 більша або менша другої
більша або менша другої 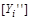 і у скільки разів унаслідок цього зменшується або збільшується числове значення
і у скільки разів унаслідок цього зменшується або збільшується числове значення 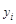 .
.
Для фізичної величини 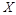 , яка пов’язана з
, яка пов’язана з 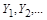 залежністю (1.4.6)
залежністю (1.4.6)
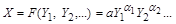 ,
,
числове значення визначається аналітичною формулою
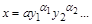
Тому в першій системі одиниць матимемо
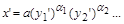 ,
,
а в другій –
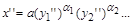 .
.
З урахуванням співвідношення (1.4.11) матимемо
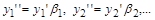
Підставимо ці значення у співвідношення для 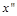 :
:
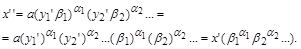
Таким чином, знаходиться коефіцієнт
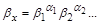 (1.4.12)
(1.4.12)
для перерахунку числового значення похідної фізичної величини 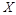 з одної системи виміру в іншу. Одержана формула (1.4.12) має таку ж структуру, як і формула (1.4.7).
з одної системи виміру в іншу. Одержана формула (1.4.12) має таку ж структуру, як і формула (1.4.7).
Приклад. Розглянемо залежність, що пов’язує шлях 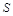 , який проходить тіло, час
, який проходить тіло, час  і швидкість
і швидкість 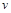 :
:
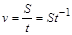 . (1.4.13)
. (1.4.13)
Розмірності шляху, часу і швидкості пов’язані аналогічною формулою:
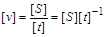 . (1.4.14)
. (1.4.14)
Розмірності 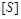 і
і 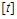 – незалежні, розмірність
– незалежні, розмірність 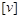 – похідна (залежна). Нехай числові значення цих величин виражаються в одиницях системи СІ, тобто відповідно в метрах, секундах і метрах за секунду (м, с, м/с). Позначимо ці числові значення
– похідна (залежна). Нехай числові значення цих величин виражаються в одиницях системи СІ, тобто відповідно в метрах, секундах і метрах за секунду (м, с, м/с). Позначимо ці числові значення 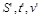 .
.
Нехай у іншій системі одиниць ці ж самі числові значення виражаються в сантиметрах, хвилинах, сантиметрах за хвилину (см, хв, см/хв). Позначимо через 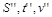 числові значення тих самих величин у другій системі одиниць виміру. При цьому
числові значення тих самих величин у другій системі одиниць виміру. При цьому
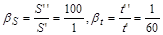 .
.
За аналогією з рівністю (1.4.14) знаходимо
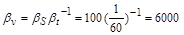 .
.
Тому
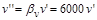 .
.
Числовий приклад. Нехай 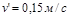 . Візьмемо в системі (м, с, м/с)
. Візьмемо в системі (м, с, м/с) 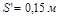 , а
, а 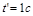 . Це дозволить отримати вказану швидкість
. Це дозволить отримати вказану швидкість 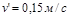 .
.
Якщо ці величини виразити в системі (см, хв, см/хв), то матимемо 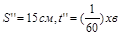 . Звідси
. Звідси  . Це дозволяє отримати
. Це дозволяє отримати
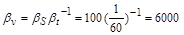 .
.
Тому
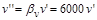 .
.
4.2. 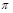 -ТЕОРЕМА
-ТЕОРЕМА
Фізична закономірність, яка визначає стан чи зміну стану будь-якого матеріального об’єкта, існує об’єктивно, незалежно від того, відома вона чи ні. Нехай математичним описанням (розрахунковою моделлю) такої фізичної закономірності є функціональна залежність
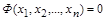 (1.4.15)
(1.4.15)
між визначальними величинами 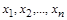 .
.
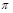 -теорема. Залежність (1.4.15), що математично виражає стан чи зміну стану матеріального об’єкта і пов’язує
-теорема. Залежність (1.4.15), що математично виражає стан чи зміну стану матеріального об’єкта і пов’язує 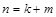 величин
величин
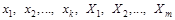 ,
,
серед яких 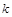 величин
величин 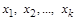 мають незалежні розмірності, може бути перетворена на залежність між
мають незалежні розмірності, може бути перетворена на залежність між 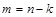 незалежними безрозмірними степеневими комплексами фізичних величин вигляду
незалежними безрозмірними степеневими комплексами фізичних величин вигляду
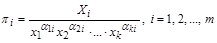 ,
,
які називаються критеріями подібності.
Доведення. Нехай у рівнянні (1.4.15) функція 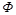 невідома, але відомі всі розмірні визначальні фізичні величини
невідома, але відомі всі розмірні визначальні фізичні величини 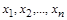 , які містяться під її знаком (у тому числі й фізичні розмірні константи). Ставиться задача: знайти критерії подібності
, які містяться під її знаком (у тому числі й фізичні розмірні константи). Ставиться задача: знайти критерії подібності 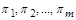 , за яких залежність (1.4.15) перетворюється на залежність
, за яких залежність (1.4.15) перетворюється на залежність
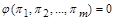 , (1.4.16)
, (1.4.16)
де 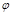 – також невідома функція.
– також невідома функція.
Незалежними розмірностями будемо вважати такі, які не можуть бути отримані у вигляді степеневих комплексів розмірностей інших величин. Наприклад, розмірності 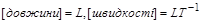 і
і 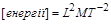 – незалежні; розмірності
– незалежні; розмірності 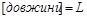 ,
, 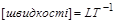 і
і 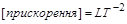 – залежні, оскільки
– залежні, оскільки
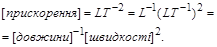
Отже, нехай серед визначальних фізичних величин 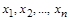 рівняння (1.4.15) незалежні розмірності мають перші
рівняння (1.4.15) незалежні розмірності мають перші 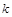 величин:
величин:
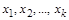 .
.
Інші 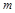 величин
величин
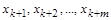
мають залежні розмірності, причому, 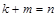 . Позначимо ці величини для зручності через
. Позначимо ці величини для зручності через
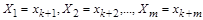 .
.
Нехай розмірності цих величин визначаються співвідношеннями
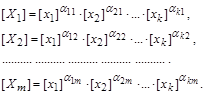
На основі цих формул можна скласти 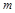 безрозмірних степеневих комплексів
безрозмірних степеневих комплексів
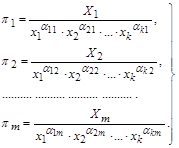 (1.4.17)
(1.4.17)
Ці комплекси називають критеріями подібності 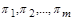 .
.
Доведемо тепер, що функціональна залежність (1.4.15)
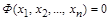
може бути приведеною до критеріальної форми (1.4.16)
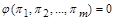 .
.
Для строгого доведення цього приймемо величини 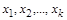 за основні й будемо виражати їх числові значення в незалежних одиницях
за основні й будемо виражати їх числові значення в незалежних одиницях 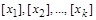 . Значення
. Значення 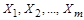 як похідних величин будемо виражати в похідних одиницях
як похідних величин будемо виражати в похідних одиницях 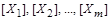 .
.
Загальна структура математичного описання фізичної закономірності не залежить від одиниць виміру визначальних фізичних величин. Однак, залежно від того, які величини вибрані за основні, у математичному описанні можуть з’явитися розмірні сталі, які належать до визначальних фізичних величин. За такої умови зі зміною розмірностей основних величин у математичному описанні змінюються тільки значення безрозмірних сталих коефіцієнтів.
Значення визначальних величин у вибраних одиницях виміру пов’язані рівнянням
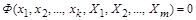 . (1.4.18)
. (1.4.18)
Змінимо розмірності одиниць виміру величин 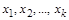 відповідно у
відповідно у 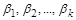 разів. Тоді нові значення
разів. Тоді нові значення 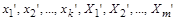 будуть дорівнювати
будуть дорівнювати
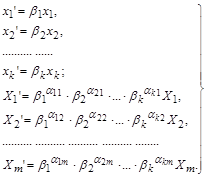 (1.4.19)
(1.4.19)
Закономірність, яка описується визначальним рівнянням (1.4.18), не залежить від вибору системи одиниць. Тому маємо
 . (1.4.20)
. (1.4.20)
Виберемо безрозмірні коефіцієнти 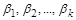 рівними
рівними
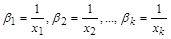 .
.
Якщо числові значення 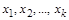 змінні, то змінними будуть і
змінні, то змінними будуть і 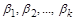 . Це означає використання незвичної системи одиниць виміру, що неперервно змінюються, системи, яка принципово завжди можлива, але очевидно у всіх випадках, крім даного, є дуже незручною. За таких умов згідно із системою (4.19) маємо
. Це означає використання незвичної системи одиниць виміру, що неперервно змінюються, системи, яка принципово завжди можлива, але очевидно у всіх випадках, крім даного, є дуже незручною. За таких умов згідно із системою (4.19) маємо
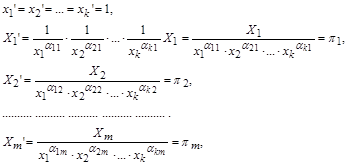
де 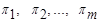 – безрозмірні степеневі комплекси – критерії подібності. Рівняння (1.4.20) набуває при цьому критеріальної форми (1.4.16):
– безрозмірні степеневі комплекси – критерії подібності. Рівняння (1.4.20) набуває при цьому критеріальної форми (1.4.16):
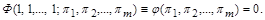
Таким чином, залежність між 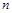 розмірних величин
розмірних величин  замінилася залежністю між
замінилася залежністю між 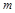 безрозмірних степеневих комплексів
безрозмірних степеневих комплексів 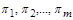 .
.
Ця доведена теорема дозволяє не використовувати при встановленні критеріїв подібності математичне описання об’єкта, який розглядається.
Приклад. Розглядається явище протікання електричного струму 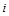 через послідовно з’єднані опір
через послідовно з’єднані опір 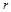 і ємність
і ємність 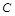 після підключення сталого напруження
після підключення сталого напруження 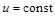 . Це явище характеризується в кожний момент часу конкретними значеннями
. Це явище характеризується в кожний момент часу конкретними значеннями 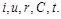
Отже, перехідний процес у 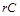 -контурі визначає залежність, що пов’язує п’ять
-контурі визначає залежність, що пов’язує п’ять 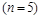 фізичних величин:
фізичних величин: 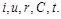 Їх розмірності в системі СІ дорівнюють
Їх розмірності в системі СІ дорівнюють
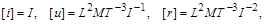
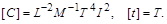
Звідси видно, що розмірності величин  і
і  виражаються через розмірності величин
виражаються через розмірності величин 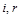 і
і 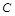 :
:
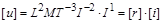 , (1.4.21)
, (1.4.21)
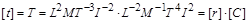 .
.
З останньої рівності маємо
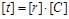 . (1.4.22)
. (1.4.22)
Тому з п’яти визначальних величин 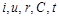 три –
три – 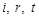 – мають незалежні розмірності. Отже, у даному випадку
– мають незалежні розмірності. Отже, у даному випадку 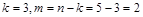 . Тому залежність між
. Тому залежність між 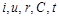 може бути заміненою залежністю між двома деякими степеневими комплексами
може бути заміненою залежністю між двома деякими степеневими комплексами 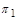 і
і 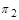 , складеними з
, складеними з 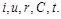 Ці комплекси на основі формул розмірності (1.4.21), (1.4.22) і системи (1.4.17) матимуть вигляд
Ці комплекси на основі формул розмірності (1.4.21), (1.4.22) і системи (1.4.17) матимуть вигляд

Таким чином, згідно з аналізом розмірностей і 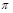 -теоремою залежність між
-теоремою залежність між 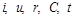 може бути зображеною у вигляді залежності між критеріями
може бути зображеною у вигляді залежності між критеріями
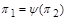 або
або 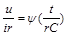 ,
,
де функція 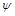 залишається невизначеною.
залишається невизначеною.
У даному випадку висновки, що отримуються на основі 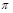 -теореми, легко перевіряються. Якщо скласти й розв’язати відповідне диференціальне рівняння об’єкта, то знайдемо
-теореми, легко перевіряються. Якщо скласти й розв’язати відповідне диференціальне рівняння об’єкта, то знайдемо
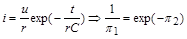 ,
,
або
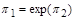 .
.
4.3. МЕТОДИКА ЗНАХОДЖЕННЯ КРИТЕРІЇВ
ПОДІБНОСТІ ЗА ВІДСУТНОСТІ
МАТЕМАТИЧНОГО ОПИСАННЯ ОБ’ЄКТА
У загальному випадку методика знаходження критеріїв подібності на основі аналізу розмірностей і 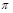 -теореми, коли математичне описання об’єкта невідоме, полягає в такому:
-теореми, коли математичне описання об’єкта невідоме, полягає в такому:
1. Установлюються всі 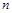 фізичних величин:
фізичних величин:
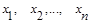 ,
,
що визначають стан або поведінку об’єкта, який розглядається.
2. Установлюються розмірності всіх 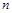 визначальних величин у будь-якій системі одиниць виміру (як правило, у системі СІ).
визначальних величин у будь-якій системі одиниць виміру (як правило, у системі СІ).
3. Розмірності одних величин виражаються через розмірності інших:
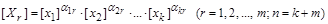 .
.
У результаті встановлюється кількість 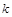 величин, які мають незалежні розмірності, і кількість критеріїв подібності
величин, які мають незалежні розмірності, і кількість критеріїв подібності 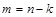 .
.
4. На основі складених формул розмірностей і згідно із системою (1.4.17) знаходять критерії подібності 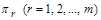 .
.
Приклад. Розглядається явище піднімання рідини всередині капілярної трубки, яка занурена в рідину.
1. Висоту підйому рідини 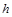 визначають внутрішній радіус трубки
визначають внутрішній радіус трубки 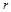 , питома вага рідини
, питома вага рідини 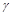 і поверхневий натяг
і поверхневий натяг 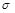 рідини.
рідини.
Отже, визначальними фізичними величинами явища є 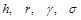 . Їхня кількість
. Їхня кількість 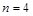 .
.
2. Розмірності визначальних величин у системі СІ є такими:
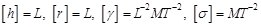 .
.
3. Складаємо формули розмірностей:
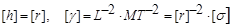 . (1.4.23)
. (1.4.23)
Звідси основними визначальними фізичними величинами є 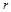 і
і 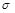 , тому що вони мають незалежні розмірності. Залежними визначальними фізичними величинами є
, тому що вони мають незалежні розмірності. Залежними визначальними фізичними величинами є 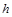 і
і 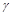 – вони мають залежні розмірності.
– вони мають залежні розмірності.
4. На основі знайдених формул розмірностей (1.4.23) отримаємо два критерії подібності:
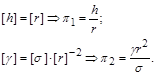
Таким чином, згідно з аналізом розмірностей і 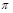 -теоремою залежність між
-теоремою залежність між 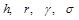 може бути зображеною у вигляді
може бути зображеною у вигляді
 .
.
Функція 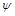 , однак, залишається невизначеною.
, однак, залишається невизначеною.
Конкретний вираз для критеріїв подібності
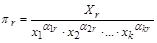
у рівнянні визначається тим, які з визначальних величин вибираються за такі, що мають незалежні розмірності. Оскільки це може бути зроблено по-різному, то форма критеріїв подібності може бути різною. Однак кожна з цих форм завжди може бути перетвореною на будь-яку іншу.
Приклад. Якщо в попередньому прикладі за величини з незалежними розмірностями вибрати не 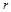 і
і 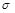 , а
, а 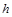 і
і 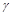 , то на основі формул розмірностей
, то на основі формул розмірностей

отримаємо інші критерії подібності:

Однак
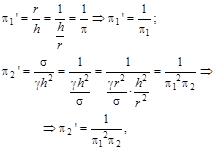
або
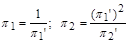 .
.
Успіх цього методу знаходження критеріїв подібності залежить від того, наскільки правильно встановлені величини, які визначають об’єктдослідження. Якщо деякі величини пропущено або вони є зайвими, то тип і кількість критеріїв подібності буде встановлено невірно.
У складних випадках, коли кількість визначальних величин є великою, найпростіший – евристичний – спосіб складання формул розмірностей для величин із залежними розмірностями і знаходження за ними критеріїв подібності є незручним і може призвести до суттєвих помилок.
Найпоширеніший метод формального характеру – це метод, який потребує складання й розв’язання деякої системи лінійних алгебраїчних рівнянь. Цей метод вивчається у більш загальних курсах лекцій з математичного моделювання.
Найзручнішим для практичного застосування є методвилучення розмірностей. Він полягає в поступовому вилученні із системи формул розмірностей визначальних величин
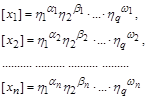
усіх символів розмірностей 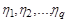 основних визначальних величин з одночасним зменшенням кількості формул з
основних визначальних величин з одночасним зменшенням кількості формул з 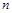 до
до 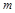 . У міру зменшення кількості формул їх праві частини спрощуються, а в лівих частинах формуються все складніші степеневі комплекси з визначальних величин. Поява, унаслідок виключення чергового символу
. У міру зменшення кількості формул їх праві частини спрощуються, а в лівих частинах формуються все складніші степеневі комплекси з визначальних величин. Поява, унаслідок виключення чергового символу 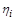 , рівності, що містить у правій частині одиницю, означає, що в лівій її частині сформовано безрозмірний степеневий комплекс – критерій подібності. Порядок виключення символів розмірностей
, рівності, що містить у правій частині одиницю, означає, що в лівій її частині сформовано безрозмірний степеневий комплекс – критерій подібності. Порядок виключення символів розмірностей 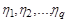 не має значення.
не має значення.
Приклад. Перехідний процес в електричному контурі, який складається з резистора, конденсатора й дроселя, при вмиканні синусоїдної напруги визначають сім величин: струм 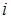 , амплітуда напруження
, амплітуда напруження 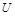 , опір
, опір 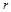 , ємність
, ємність 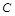 , індуктивність
, індуктивність 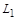 , час
, час  і частота
і частота 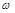 . Отже,
. Отже, 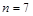 . Випишемо формули розмірностей усіх семи визначальних величин у системі СІ:
. Випишемо формули розмірностей усіх семи визначальних величин у системі СІ:
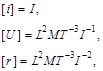

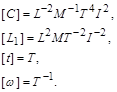
Виключимо з формул розмірностей символ 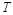 – розмірність часу
– розмірність часу  . Для цього поставимо собі питання: на скільки треба помножити
. Для цього поставимо собі питання: на скільки треба помножити 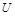 , щоб добуток у формулі розмірностей не містив символу розмірності часу
, щоб добуток у формулі розмірностей не містив символу розмірності часу 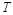 ? Ураховуючи, що формула розмірності для
? Ураховуючи, що формула розмірності для 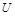 містить
містить 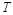 у степені (-3), отримаємо, що
у степені (-3), отримаємо, що 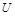 слід помножити на
слід помножити на 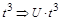 , тоді
, тоді 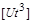 не буде містити в правій частині символ
не буде містити в правій частині символ 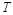 – розмірність часу
– розмірність часу  . Отже,
. Отже, 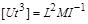 . Зробимо те саме з усіма іншими формулами розмірностей. Отримаємо
. Зробимо те саме з усіма іншими формулами розмірностей. Отримаємо