
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВПЦ “Київський університет”, 2006 6 страница
|
|
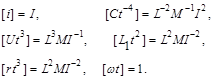
У результаті знаходимо перший критерій подібності 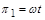 .
.
Виключимо 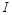 з п’яти формул, що залишилися, – це символ розмірності струму
з п’яти формул, що залишилися, – це символ розмірності струму  :
:
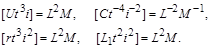
Тепер виключимо 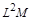 . З перших двох формул випливає
. З перших двох формул випливає
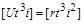 . (1.4.24)
. (1.4.24)
З першої і третьої –
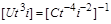 . (1.4.25)
. (1.4.25)
З першої і четвертої –
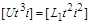 . (1.4.26)
. (1.4.26)
Звідси ми знаходимо ще три критерії. З рівності (1.4.24) випливає, що добутки 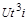 і
і 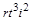 мають однакові розмірності. Тому при діленні одного з них на другий ми отримаємо безрозмірний комплекс
мають однакові розмірності. Тому при діленні одного з них на другий ми отримаємо безрозмірний комплекс
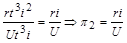 .
.
Аналогічно з формули (1.4.25) видно, що добутки 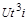 і
і 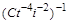 мають однакові розмірності. Звідси отримується ще один безрозмірний комплекс. Поділимо
мають однакові розмірності. Звідси отримується ще один безрозмірний комплекс. Поділимо 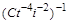 на
на 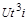
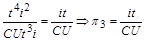 .
.
Аналогічно з рівності (1.4.26)
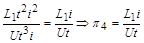 .
.
4.4. РОЗРАХУНКОВЕ МОДЕЛЮВАННЯ
ЗА ДОПОМОГОЮ КРИТЕРІЇВ ПОДІБНОСТІ
Можливість приведення залежності між 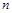 розмірних величин
розмірних величин 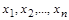 до залежності між
до залежності між 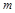 безрозмірних критеріїв подібності
безрозмірних критеріїв подібності 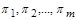 дозволяє при
дозволяє при 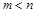 спростити (часто дуже суттєво) знаходження математичного описання різних об’єктів, тобто здійснити розрахункове моделювання.
спростити (часто дуже суттєво) знаходження математичного описання різних об’єктів, тобто здійснити розрахункове моделювання.
Експериментальне встановлення залежності
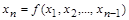 (1.4.27)
(1.4.27)
за великих 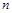 потребує великої кількості дослідних даних. Так, для табулювання функції однієї змінної необхідно два рядки, функції двох змінних – сторінка, при трьох аргументах – книга, а при чотирьох – уже ціла бібліотека. Обробка цих даних з метою отримання аналітичного виразу функції
потребує великої кількості дослідних даних. Так, для табулювання функції однієї змінної необхідно два рядки, функції двох змінних – сторінка, при трьох аргументах – книга, а при чотирьох – уже ціла бібліотека. Обробка цих даних з метою отримання аналітичного виразу функції 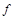 є складною й трудомісткою.
є складною й трудомісткою.
У той же час експериментальне встановлення критеріальної залежності
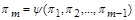 (1.4.28)
(1.4.28)
за малих 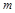 може бути зовсім простим.
може бути зовсім простим.
У випадку розрахункового моделювання матеріальних об’єктів за допомогою аналізу розмірностей і 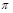 -теореми дуже важливою є форма критеріїв подібності, яка в загальному випадку може бути різною.
-теореми дуже важливою є форма критеріїв подібності, яка в загальному випадку може бути різною.
Кілька порад:
1. З усіх можливих варіантів форми критеріїв подібності кращим є той, якому відповідає найпростіший вираз функції (1.4.28).
2. Підставою для вибору форми критеріїв подібності можуть служити міркування зручності планування експериментів.
3. У всіх випадках доцільно вибирати такі форми критеріїв подібності, які мають певний фізичний зміст.
Приклад. Тіло з певною формою поверхні, розміри якого визначає деякий характерний відрізок 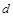 , наприклад, підводний човен, поперечним перерізом якого є коло діаметром
, наприклад, підводний човен, поперечним перерізом якого є коло діаметром 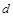 , рухається зі швидкістю
, рухається зі швидкістю 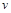 у рідині з коефіцієнтом динамічної в’язкості
у рідині з коефіцієнтом динамічної в’язкості 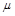 і густиною
і густиною 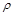 . Необхідно встановити силу лобового опору
. Необхідно встановити силу лобового опору
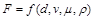 ,
,
який зазнає тіло.
Розмірності вказаних 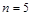 визначальних величин у системі СІ є такими:
визначальних величин у системі СІ є такими:
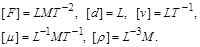
Оскільки необхідно знайти залежність 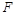 від
від 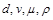 у явному вигляді, то
у явному вигляді, то 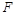 приймемо за величину із залежною розмірністю і знайдемо
приймемо за величину із залежною розмірністю і знайдемо
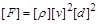 . (1.4.29)
. (1.4.29)
Іншою величиною із залежною розмірністю є 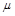 . Для неї отримаємо
. Для неї отримаємо
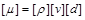 . (1.4.30)
. (1.4.30)
Таким чином, 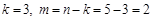 і два критерії подібності згідно з (1.4.29) і (1.4.30) будуть
і два критерії подібності згідно з (1.4.29) і (1.4.30) будуть
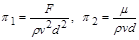 .
.
Якщо прийняти за величини із залежними розмірностями 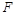 і
і 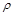 , то отримаємо
, то отримаємо
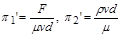 .
.
Якщо за величини із залежними розмірностями прийняти 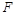 і
і 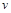 , то матимемо
, то матимемо
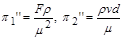 .
.
Такий самий результат дає випадок, коли величинами із залежними розмірностями вибираються 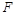 і
і 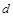 .
.
Таким чином, у всіх розглянутих варіантах другий критерій подібності залишається практично незмінним.
Безрозмірний степеневий комплекс 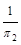 зустрічається в багатьох задачах гідромеханіки й має певний фізичний зміст: його числове значення характеризує співвідношення між силами інерції й силами тертя в потоці в’язкої рідини. Цей комплекс називається критерієм або числом Рейнольдса і позначається
зустрічається в багатьох задачах гідромеханіки й має певний фізичний зміст: його числове значення характеризує співвідношення між силами інерції й силами тертя в потоці в’язкої рідини. Цей комплекс називається критерієм або числом Рейнольдса і позначається
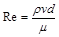 .
.
Із трьох критеріїв  певний фізичний зміст має тільки один критерій
певний фізичний зміст має тільки один критерій  . Він характеризує відношення лобового опору до сили, яка виникає внаслідок тиску рідини на лобову поверхню. Якщо вибрати цей критерій, то отримаємо критеріальне рівняння
. Він характеризує відношення лобового опору до сили, яка виникає внаслідок тиску рідини на лобову поверхню. Якщо вибрати цей критерій, то отримаємо критеріальне рівняння 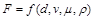 у вигляді
у вигляді
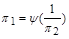 , (1.4.31)
, (1.4.31)
звідки
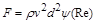 .
.
Із цього виразу перед усім випливає, що вплив в’язкості рідини виявляється тільки через число Рейнольдса. Чим більша в’язкість 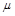 , тим менше
, тим менше 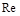 і більше
і більше 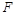 . Значить, при зменшенні
. Значить, при зменшенні 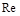 функція (1.4.31) має зростати. Зі зменшенням в’язкості
функція (1.4.31) має зростати. Зі зменшенням в’язкості 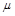 число
число 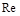 збільшується. Функція
збільшується. Функція 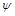 із зростанням
із зростанням 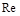 має прямувати до деякої межі при
має прямувати до деякої межі при 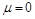 , що відповідає ідеальній рідині. При русі тіла в ідеальній рідині лобовий опір є пропорційним густині
, що відповідає ідеальній рідині. При русі тіла в ідеальній рідині лобовий опір є пропорційним густині 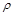 рідини, квадрату швидкості
рідини, квадрату швидкості 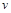 руху тіла й площі
руху тіла й площі 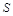 його лобової поверхні. Для в’язкої рідини такий закон зберігається наближено при достатньо великих значеннях
його лобової поверхні. Для в’язкої рідини такий закон зберігається наближено при достатньо великих значеннях 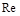 .
.
ЧАСТИНА 2
ПРИКЛАДИ ПОБУДОВИ
МАТЕМАТИЧНИХ МОДЕЛЕЙ
Перейдемо до побудови й дослідження конкретних математичних моделей із застосуванням викладеної вище теоретичної бази. На прикладах проілюструємо прийоми й методи математичного моделювання.
1. БІОЛОГІЧНІ МОДЕЛІ
Будь-яку кінетичну біологічну систему можна охарактеризувати як сукупність деяких параметрів, значення яких підтримуються незмінними протягом часу спостереження за системою, та змінних у часі. Параметрами є, наприклад, такі фізичні величини, як температура, вологість, електрична провідність мембрани, рН і т. д. Залежно від досліджуваних біосистем змінними вважаються: в екології – чисельність виду, у біофізиці – мембранний потенціал, у мікробіології – кількість мікроорганізмів, у біохімії – концентрація речовини тощо.
Припустимо, що в біосистемі є 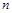 різних компонент (напр., хімічних сполук), які з часом зазнають метаболічних перетворень. Це означає, що значення концентрації
різних компонент (напр., хімічних сполук), які з часом зазнають метаболічних перетворень. Це означає, що значення концентрації 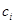 кожної
кожної 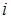 -ї сполуки (
-ї сполуки (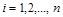 ) змінюється з часом унаслідок її взаємодії з будь-якою іншою (
) змінюється з часом унаслідок її взаємодії з будь-якою іншою (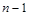 ) компонентою. Такого припущення достатньо для побудови загальної математичної моделі, яка є системою
) компонентою. Такого припущення достатньо для побудови загальної математичної моделі, яка є системою 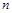 диференціальних рівнянь першого порядку
диференціальних рівнянь першого порядку
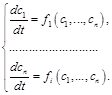 (2.1.1)
(2.1.1)
У системі (2.1.1), де 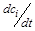
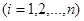 –швидкості зміни невідомих концентрацій (змінних),
–швидкості зміни невідомих концентрацій (змінних), 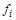 – деякі функції, які можуть залежати як від внутрішніх (напр., рН), так і від зовнішніх (напр., температура) параметрів біосистеми.
– деякі функції, які можуть залежати як від внутрішніх (напр., рН), так і від зовнішніх (напр., температура) параметрів біосистеми.
Знайти загальний розв'язок моделі (2.1.1) в аналітичному вигляді, як правило, вдається лише тоді, коли вона є лінійною. Однак процеси, які відбуваються в біологічних системах, як правило, є нелінійними; відповідно нелінійними є й математичні моделі цих процесів. Проте існують методи якісного аналізу диференціальних рівнянь, які дають можливість виявити важливі загальні властивості (закономірності) моделі (2.1.1), не знаходячи в явному вигляді невідомі функції 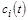 .
.
Ці методи базуються на таких експериментальних фактах. По-перше, різні функціональні процеси в біосистемах суттєво відрізняються один від одного за часом проходження або характерними швидкостями. Так, наприклад, у біосистемі одночасно мають місце швидкі процеси ферментативного каталізу (час обороту ферменту становить 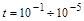 с), фізіологічні процеси (час – хвилини) та процеси репродукції (від кількох хвилин і більше). По-друге, якщо окремі (проміжні) стадії загального процесу в біосистемі характеризуються часом
с), фізіологічні процеси (час – хвилини) та процеси репродукції (від кількох хвилин і більше). По-друге, якщо окремі (проміжні) стадії загального процесу в біосистемі характеризуються часом 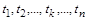 і найповільніша стадія має час
і найповільніша стадія має час 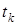 такий, що
такий, що 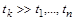 , то визначальною ланкою всього процесу є
, то визначальною ланкою всього процесу є 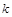 -та стадія, і загальний час проходження процесу практично збігається з
-та стадія, і загальний час проходження процесу практично збігається з  . Отже, наявність такої часової ієрархії процесів у біосистемі дає можливість значно спростити вихідну модель, звівши її, по суті, до кінетичного опису поведінки найбільш повільної стадії.
. Отже, наявність такої часової ієрархії процесів у біосистемі дає можливість значно спростити вихідну модель, звівши її, по суті, до кінетичного опису поведінки найбільш повільної стадії.
Як видно з рівнянь (2.1.1), зміна стану системи описується деякою точкою  у
у 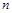 -мірному просторі значень змінних
-мірному просторі значень змінних 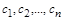 . Простір з координатами
. Простір з координатами 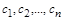 називається фазовим. Крива, яку описує в цьому просторі точка
називається фазовим. Крива, яку описує в цьому просторі точка 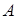 , називається фазовою траєкторією.
, називається фазовою траєкторією.
Однією з важливих властивостей відкритих систем (на відміну від ізольованих) є наявність у них стаціонарних станів. За означенням, у стаціонарному стані
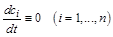 . (2.1.2)
. (2.1.2)
У результаті отримуємо систему алгебраїчних рівнянь для визначення стаціонарної (особливої) точки фазового простору 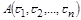 :
:
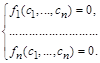 (2.1.3)
(2.1.3)
Динамічні біосистеми, які описуються за допомогою звичайних диференціальних рівнянь типу (2.1.1), називаються точковими системами. Це означає, що в будь-якій точці такої системи значення шуканої величини (напр., концентрації речовини) зберігається з часом. Однак загальнішим є випадок, коли значення змінних є різними в різних точках простору. Наприклад, коли одночасно з реакцією, яка відбувається на деякій ділянці системи, реагенти дифундують, переходячи до іншої ділянки. Кінетичні рівняння, які враховують дифузійний зв’язок між окремими ділянками простору в біосистемі, мають вигляд
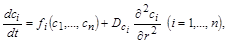 (2.1.4)
(2.1.4)
де 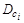 – коефіцієнт дифузії речовини
– коефіцієнт дифузії речовини 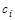 ,
, 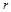 – просторова координата.
– просторова координата.
Система рівнянь (2.1.4) дає можливість пояснити деякі загальні принципи процесів самоорганізації в живих організмах.
1.2. ПОПУЛЯЦІЙНІ МОДЕЛІ
Побудуємо й дослідимо математичні моделі, що описують зміну чисельності біологічних популяцій. Від найпростіших одновидових популяцій перейдемо до складніших, багатовидових популяцій з урахуванням дедалі більшого числа факторів, що впливають на зміну чисельності в популяціях. Побудуємо ієрархічний ланцюг у даних моделях. Коротко опишемо сучасний стан проблеми, укажемо на питання, що є актуальними для цієї теорії і розв’язання яких може бути темою подальших наукових досліджень або кваліфікаційних робіт з математичного моделювання.
1.2.1. Модель Мальтуса одновидової популяції
Розглянемо модель одновидової біологічної популяції. Через 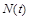 позначимо кількість особин у момент часу
позначимо кількість особин у момент часу  . Наша мета – вивести закон зміни кількості особин із часом. Для цього, згідно з принципами математичного моделювання, зробимо деякі спрощувальні припущення. А саме: будемо вважати, що дана популяція існує ізольовано й на деякій території розміщена однорідно. Пізніше ми ці припущення дещо послабимо.
. Наша мета – вивести закон зміни кількості особин із часом. Для цього, згідно з принципами математичного моделювання, зробимо деякі спрощувальні припущення. А саме: будемо вважати, що дана популяція існує ізольовано й на деякій території розміщена однорідно. Пізніше ми ці припущення дещо послабимо.
Виберемо закон, згідно з яким відбувається розвиток популяцій. За основу візьмемо відомий закон Мальтуса: швидкість зміни популяції пропорційна величині популяції з певним коефіцієнтом, що є різницею між коефіцієнтом народжуваності 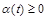 і смертності
і смертності 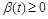 . За цих припущень можна отримати закон зміни чисельності популяцій, що в математичній формі має вигляд
. За цих припущень можна отримати закон зміни чисельності популяцій, що в математичній формі має вигляд
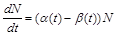 . (2.1.5)
. (2.1.5)
З формули (2.1.5) можна зробити висновки про зміни чисельності з часом. Так, якщо 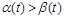 (миттєва народжуваність більша за миттєву смертність), то
(миттєва народжуваність більша за миттєву смертність), то 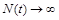 при
при 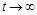 ; якщо
; якщо 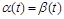 , то
, то 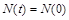 – чисельність із часом не змінюється; якщо
– чисельність із часом не змінюється; якщо 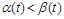 – чисельність популяції прямує до нуля.
– чисельність популяції прямує до нуля.
З математичного погляду дана модель є дуже зручною, оскільки її можна повністю дослідити. Зокрема, з неї випливає результат, який ще у 1798 р. отримав Мальтус і запропонував свою “похмуру теорію”: людство може вижити, тільки якщо періоди зростання в геометричній прогресії будуть перериватися епідеміями, війнами й стихійними лихами. Дійсно, це той випадок, коли 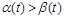 і
і 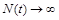 при
при 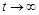 . Насправді це не так. Модель Мальтуса дуже наближено відповідає оригіналу, коли інтервали часу є невеликими. Її можна розглядати лише як перше наближення до реального процесу.
. Насправді це не так. Модель Мальтуса дуже наближено відповідає оригіналу, коли інтервали часу є невеликими. Її можна розглядати лише як перше наближення до реального процесу.
Дуже складний процес зміни чисельності населення, залежний до того ж від свідомого втручання самих людей, не може описуватись простими законами. Навіть в ідеальному випадку ізольованої біологічної популяції запропонована модель не відповідає реальності повною мірою хоча б через обмеженість ресурсів, необхідних для її існування. З цього випливає так званий ефект насичення.
Вправа. За яких умов на 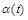 і
і  є:
є:
1) обмеженою при 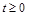 ;
;
2) періодичною?
1.2.2. Модель одновидової популяції
з урахуванням насичення (логістична модель)
Більш точна модель має враховувати конкурентну боротьбу в обмеженому життєвому просторі. Зробимо відносно моделі таке припущення, що підтверджується практичними спостереженнями: середньостатистична кількість попарних сутичок у популяції за одиницю часу пропорційна 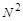 . Тоді рівняння балансу “зміна кількості” = “приріст” – “втрати” можна подати у вигляді
. Тоді рівняння балансу “зміна кількості” = “приріст” – “втрати” можна подати у вигляді
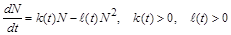 . (2.1.6)
. (2.1.6)
Це рівняння вивів у 1837 р. данський учений Ферхюльст. Воно називається логістичним і є математичною моделлю одновидової популяції з урахуванням ефекту насичення.
Проаналізуємо дану математичну модель. Основна вимога до неї – досить точно описувати реальний процес за великих значень  . З математичного погляду цій вимозі відповідає нелінійне рівняння Ріккатті, загальний розв’язок якого може бути знайденим у квадратурах шляхом його зведення до лінійного. Однак точні формули виявляються досить громіздкими для практичного користування. Проте нас цікавить лише асимптотична поведінка розв’язків при
. З математичного погляду цій вимозі відповідає нелінійне рівняння Ріккатті, загальний розв’язок якого може бути знайденим у квадратурах шляхом його зведення до лінійного. Однак точні формули виявляються досить громіздкими для практичного користування. Проте нас цікавить лише асимптотична поведінка розв’язків при 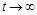 . Таке дослідження у випадку, коли
. Таке дослідження у випадку, коли 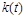 і
і 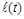 є сталими, можна провести й без інтегрування рівняння (2.1.6).
є сталими, можна провести й без інтегрування рівняння (2.1.6).
Заміною змінних  і
і 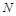 рівняння (2.1.6) можна звести до вигляду
рівняння (2.1.6) можна звести до вигляду
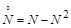 , (2.1.7)
, (2.1.7)
тобто коефіцієнти 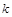 і
і 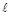 можна вважати рівними 1.
можна вважати рівними 1.
Розв’язки залежать від зміни знаків функції 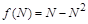 . Очевидно, що
. Очевидно, що 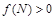 при
при 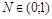 і
і 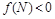 при
при 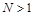 (нас цікавить випадок
(нас цікавить випадок 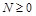 ).
).
Отже, дане рівняння має два положення рівноваги:  і
і 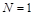 , причому перше з них є нестійким, а друге – асимптотично стійким, усі розв’язки при
, причому перше з них є нестійким, а друге – асимптотично стійким, усі розв’язки при 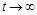 наближуються до нього. Поведінку інтегральних кривих зображено на рис. 2.1.1.
наближуються до нього. Поведінку інтегральних кривих зображено на рис. 2.1.1.
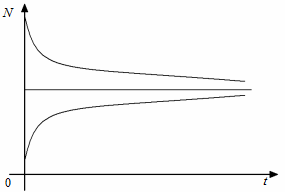
Рис. 2.1.1
Отже, у логістичній моделі всі розв’язки з часом прямують до рівноважного стану, і ніякого перенаселення, як стверджував Мальтус, бути не може.
1.2.3. Логістична модель з урахуванням зовнішніх впливів
Описані вище моделі будувалися на припущенні, що популяція існує ізольовано й не зазнає жодних зовнішніх впливів. Це припущення, зрозуміло, значно понижує степінь адекватності даної моделі оригіналу. Побудуємо більш складну модель, що враховує зовнішній вплив. Вона буде наступною ланкою в ієрархічному ланцюзі моделей популяцій, побудованому за принципом знизу-вверх (від простої моделі – до більш складної).
Якщо мова йде, наприклад, про популяцію риб у водоймі, то зовнішній вплив може означати постійне їх відловлення.
Будемо вважати, що швидкість вилучення особин з популяції є сталою, тоді, за аналогією з попереднім, математичною моделлю даного об’єкта є рівняння
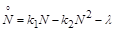 (2.1.8)
(2.1.8)
Покладемо, що 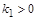 і
і 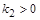 рівні 1. Отримаємо рівняння
рівні 1. Отримаємо рівняння
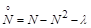 , (2.1.9)
, (2.1.9)
де 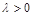 – параметр, що відповідає за швидкість вилучення. Розглянемо його вплив на процес розвитку популяції.
– параметр, що відповідає за швидкість вилучення. Розглянемо його вплив на процес розвитку популяції.
При 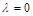 – це описана вище логістична модель. При зростанні
– це описана вище логістична модель. При зростанні 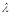 відбувається зближення положень рівноваги
відбувається зближення положень рівноваги 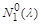 і
і 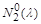 , які є функціями
, які є функціями 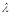 , але їх характер не змінюється, як і в логістичній моделі (рис. 2.1.2).
, але їх характер не змінюється, як і в логістичній моделі (рис. 2.1.2).
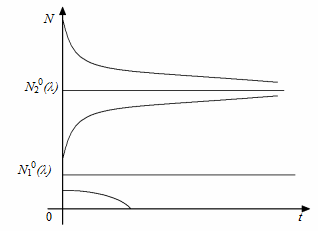
Рис. 2.1.2
При критичному значенні 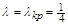 положення рівноваги зливаються в одне кратне положення рівноваги (рис. 2.1.3).
положення рівноваги зливаються в одне кратне положення рівноваги (рис. 2.1.3).
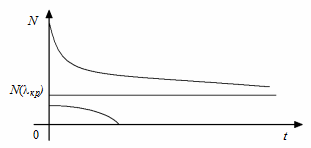
Рис. 2.1.3
При подальшому зростанні 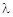 рівняння (2.1.9) не матиме положень рівноваги, і популяція з часом зникне (рис. 2.1.4).
рівняння (2.1.9) не матиме положень рівноваги, і популяція з часом зникне (рис. 2.1.4).
 Рис. 2.1.4
Рис. 2.1.4
Тобто сильний зовнішній вплив, наприклад, відловлення риб, може призвести до зникнення виду, як це трапилося з турами, стелеровою коровою тощо.
Якісна зміна поведінки системи при проходженні параметром  критичного значення
критичного значення  називається біфуркацією; вона відображає явище фазового переходу в біологічній системі (популяції).
називається біфуркацією; вона відображає явище фазового переходу в біологічній системі (популяції).
Небезпечними для виживання популяції, незалежно від її початкової величини, є не тільки значення 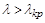 , а й усі значення
, а й усі значення 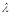 , досить близькі до критичного. Дійсно, на перший погляд, якщо
, досить близькі до критичного. Дійсно, на перший погляд, якщо 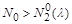 ,
,  то
то 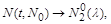 при
при 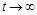 , і популяції вимирання не загрожує. Однак якщо
, і популяції вимирання не загрожує. Однак якщо 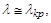 то
то 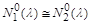 , і найменша випадкова флуктуація величини популяції
, і найменша випадкова флуктуація величини популяції 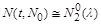 (t – досить велике) може зробити цю величину меншою за
(t – досить велике) може зробити цю величину меншою за 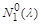 , що спричинить вимирання популяції.
, що спричинить вимирання популяції. 
1.2.4. Модель двовидової популяції Лотки – Вольтерра
Від моделі одновидової популяції перейдемо до наступної в ієрархічному ланцюзі популяцій ланки, коли існує кілька біологічних видів. Найпростішим випадком такої ситуації є двовидова популяція типу “хижак-жертва”. Нехай скалярні змінні x та y характеризують величини популяцій хижаків і жертв відповідно. При побудові математичної моделі зробимо такі спрощувальні припущення:
а) за відсутності хижаків жертви розвиваються згідно з логістичним рівнянням (2.1.6);
б) за наявності хижаків додаткові втрати жертв пропорційні як їх кількості, так і кількості хижаків (отже, у правій частині рівняння (2.1.6) потрібно дописати вираз 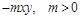 );
);