ВПЦ “Київський університет”, 2006 9 страница

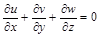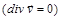, . (2.3.33)

Якщо ввести функцію напору (п’єзометричного напору)

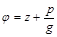, (2.3.34)

то рівняння фільтрації (2.3.31 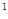) матимуть вигляд

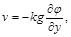
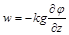. (2.3.35)

Підставляючи (2.3.35) у (2.3.33), запишемо рівняння для знаходження напору :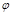

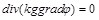. (2.3.36)

Якщо 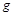і 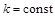, то воно зводиться до рівняння Лапласа:

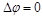. (2.3.37)

Тут частинки нестисливої рідини рухаються лініями току, що ортогональні до поверхонь сталого напору:

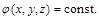(2.3.38)

Рівняння фільтрації політропного газу. Рівняння стану такого газу має вигляд

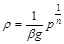, (2.3.39)

де 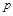– абсолютний тиск газу, 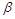– стала газу, 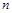– показник політропи. Підставляючи (2.3.39) у рівняння фільтрації (2.3.32) і нехтуючи в ньому малими силами ваги, отримаємо рівняння

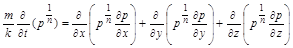. (2.3.40)

Якщо ввести заміну , то ,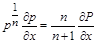

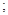
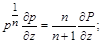
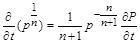і рівняння (2.3.40) набуде вигляду

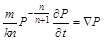. (2.3.41)

Це і є основне рівняння фільтрації політропного газу в пористому середовищі (Лейбензона). При його інтегруванні необхідно задати початкову

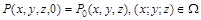
та крайову

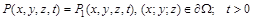
умови.

Рівняння Бусінеска. Однією з основних модельних задач руху ґрунтових вод є задача плоскої фільтрації рідини в пласті. Пласт, яким рухається рідина, має знизу непроникний ґрунт. Вода займає лише частину пласта й має вільну поверхню, тиск над якою є сталим. При відкачуванні води з пласта через водозбірні криниці або свердловини її початковий рівень у пласті змінюється, і рівень вільної поверхні води знижується в напрямку стоку. Припустимо, що висота вільної поверхні в пласті, що розташований під площиною відліку, описується функцією координат 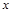та 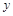, яка змінюється неперервно й дуже повільно протягом усього пласта, а глибина дна 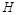також є неперервною функцією від 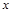та 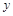, що дуже повільно змінюється протягом усього пласта. Ці припущення дозволяють вважати рух рідини плоским, тобто таким, що всі величини, які його характеризують, залежать лише від 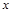та 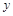, а вертикальна складова швидкості фільтрації .

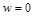Математичною моделлю такої плоскої фільтрації є диференціальне рівняння Бусінеска відносно п’єзометричного напору :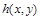

,

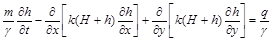де 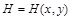– глибина дна пласта, 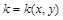– коефіцієнт фільтрації, 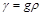– питома вага, 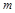– пористість шару, 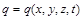– густина осадів.

Якщо 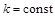, то при 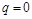маємо рівняння

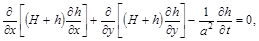(2.3.42)

де .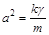

Розглянемо деякі окремі випадки рівняння (2.3.42):

1. Якщо відношення 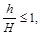то в рівнянні (2.3.42) можна знехтувати напором 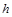порівняно з глибиною 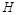, що приводить до лінійного рівняння із змінними коефіцієнтами

.

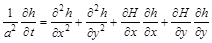Коли рух усталиться, отримаємо стаціонарне рівняння

.

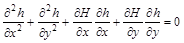2. Якщо підстильний пласт горизонтальний, то його можна прийняти за горизонтальну площину 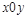і взяти 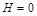. Тоді рівняння (2.3.42) матиме вигляд

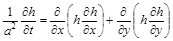
або

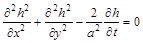. (2.3.43)

Це важливе рівняння було отримано Буссінеском.

Якщо рух є стаціонарним, то маємо

.

Це рівняння Дюпюї.

3. Проведемо аналогію з рухом газу. Якщо процес фільтрації газу ізотермічний, то показник політропи 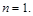Тоді рівняння (2.3.40) має вигляд

.

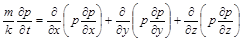Якщо рух газу плоский, то отримаємо рівняння

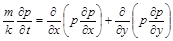
або

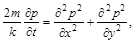
яке збігається з рівнянням (2.3.41).

Одномірні нелінійні крайові задачі нестаціонарної ізотермічної фільтрації рідин і газів у пористих середовищах. До таких задач ми приходимо у випадку, коли процес фільтрації залежить тільки від однієї просторової змінної та часу 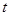. Така властивість притаманна процесам із плоскою, циліндричною або сферичною симетрією.

Тоді рівняння (2.3.32) можна записати у вигляді

, (2.3.44)

де 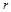– просторова координата, тобто відстань: а) від даної точки пористого середовища до площини відліку при русі газу плоскими хвилями; б) від цієї точки до осі симетрії руху при осесиметричному русі газу; в) від точки до центра симетрії при центрально-симетричному русі газу. Відповідно 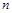дорівнює 1, 2 або 3 для цих типів руху.

Якщо 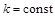, то для політропного газу отримаємо рівняння

.

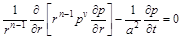ЛІТЕРАТУРА

1. Березовский А.А. Лекции по нелинейным краевым задачам математической физики. – К., 1974. – Ч. І, ІІ.

2. Веников В.А. Теория подобия и моделирования. – М., 1976.

3. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. – К., 1974.

4. Гихман И.И., Скороход А.В. Стохастические дифференциальные уравнения. – К., 1968.

5. Краснощеков П.С., Петров А.А. Принципы построения моделей. – М., 1983.

6. Самарский А.А., Михайлов А.П. Математическое моделирование. Идеи. Методы. Примеры. – 2-е изд., исправл. – М., 2001.

Зміст

ЧАСТИНА 1
ОСНОВНІ ПРИНЦИПИ ПОБУДОВИ МАТЕМАТИЧНИХ МОДЕЛЕЙ

1. ТЕОРЕТИЧНІ ОСНОВИ МОДЕЛЮВАННЯ........................................................... 3

1.1. Вступ..................................................................................................................... 3

1.2. Основні категорії теорії моделювання......................................................... 4

1.3. Класифікація видів подібності та моделювання....................................... 9

2. МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ...................................................................... 12

2.1. Вступ................................................................................................................... 12

2.2. Математичні моделі та основні заходи

математичного моделювання............................................................................. 13

3. ЗАСТОСУВАННЯ ТЕОРІЇ ПОДІБНОСТІ ПРИ ПОБУДОВІ МАТЕМАТИЧНИХ МОДЕЛЕЙ 31

3.1. Знаходження критеріїв подібності явища за наявності його математичної моделі 31

3.2. Теореми подібності........................................................................................ 37

4. МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ЗА ВІДСУТНОСТІ МОДЕЛЬНОГО ДИФЕРЕНЦІАЛЬНОГО РІВНЯННЯ 43

4.1. Розмірності....................................................................................................... 43

4.2. 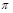-теорема........................................................................................................ 50

4.3. Методика знаходження критеріїв подібності за відсутності математичного описання об’єкта 54

4.4. Розрахункове моделювання за допомогою критеріїв подібності...... 58

ЧАСТИНА 2

ПРИКЛАДИ ПОБУДОВИ МАТЕМАТИЧНИХ МОДЕЛЕЙ

1. БІОЛОГІЧНІ МОДЕЛІ................................................................................................ 61

1.2. Популяційні моделі......................................................................................... 63

2. МОДЕЛІ ДЕЯКИХ ФІНАНСОВИХ І СТРАХОВИХ ПРОЦЕСІВ........................ 74

2.1. Математична модель роботи страхової компанії.................................. 74

2.2. Моделювання ринку фінансів...................................................................... 78

3. НЕЛІНІЙНІ МОДЕЛІ ТЕПЛОПРОВІДНОСТІ ТА ФІЛЬТРАЦІЇ........................... 81

3.1. Розповсюдження тепла при теплопровідності, що залежить від температури 81

3.2. Рівняння фільтрації........................................................................................ 88

ЛІТЕРАТУРА................................................................................................................... 94

Навчальне видання

СТАНЖИЦЬКИЙ Олександр Миколайович
ТАРАН Євген Юрійович
ГОРДИНСЬКИЙ Любомир Дмитрович