
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однопараметрические модели.
|
|
Такие модели дают описание турбулентности с помощью одной переменной, для которой строится дифференциальное уравнение переноса. Другие характеристики турбулентности определяются через нее с помощью алгебраических соотношений. К однопараметрическим моделям относятся модели Колмогорова-Прандтля, Брэдшоу, Гуляева, Козлова, Секундова и др.
Рассмотрим однопараметрическую модель Спалларта-Аллмареса. Эта модель конструировалась прежде всего для задач внешней аэродинамики и создана она была сравнительно недавно (конец 90-х). Уравнение для вихревой вязкости в этой модели записывается

Коэффициенты и замыкающие функции записываются

Тензор Ω ij = 0, 5(∂ ui/∂ xj - ∂ uj /∂ xi) - тензор вращения, а d - расстояние от
ближайшей стенки. Следует обратить внимание на то, что источниковые члены в
уравнении для турбулентной вязкости зависят от расстояния до ближайшей стенки,
а также от градиента турбулентной вязкости. При удалении от стенки модель пред-
сказывает не распадающуюся турбулентную вязкость в невозмущенном потоке.
Опыт эксплуатации модели SA показал, что ее реальные возможности заметно
шире, чем предполагалось при ее создании. Более того, после введения в нее по-
правок на кривизну линий тока и вращение, границы ее применимости модели заметно расширились.
В табл. 5.1 сведены результаты отклонений рассчитанных с помощью SA и измеренных коэффициентов трения в эталонных градиентных течениях.
В табл. 5.1 сведены результаты отклонений рассчитанных с помощью SA и измеренных коэффициентов трения в эталонных градиентных течениях.
Таблица 5.1
| Градиент давления | Течения | Спалларт-Аллмарес |
| Отрицательный | 1400, 1300, 2700, 6300 | 1.4% |
| Умеренный положительный | 1100, 2100, 2500, 4800 | 9.9% |
| Малый положительный | 2400, 2600, 3300, 4500 | 11.0% |
| Сильный положительный | 0141, 1200, 4400 | 7.2% |
| В целом | - | 7.4% |
Обнаружено, что предсказанный с помощью SA коэффициент трения так же близко
соответствует измеренным величинам, как и алгебраическая модель Болдуина-
Ломакса.
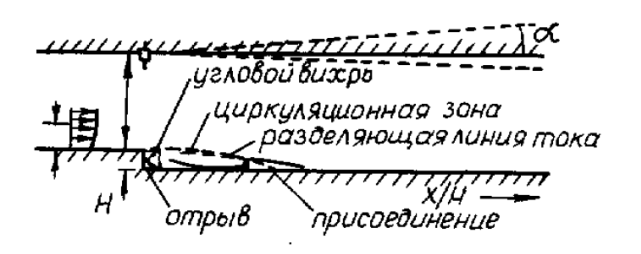
Известно, что задача об обтекании обращенной назад ступеньки является весь-
ма популярным тестом для анализа моделей турбулентности. На рис.19 показана
схема одного из экспериментов, выполненных Драйвером и Сигмюллером (1985).
Важным свойством рассматриваемого типа течения является то, что точка отрыва
оказывается фиксированной в острой кромке ступенчатого канала. Гораздо сложнее
прогнозировать течения с априори неизвестной точкой отрыва.
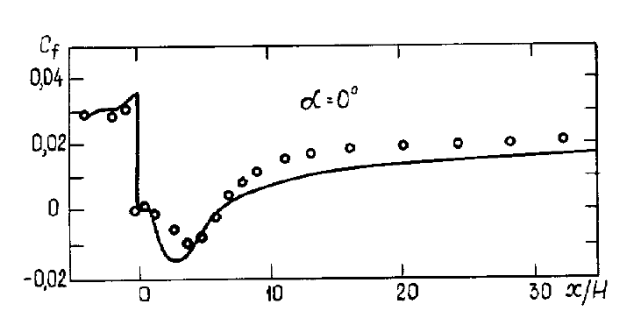
На рис. 20 сравниваются расчетные и измеренные коэффициенты трения вдоль
нижней стенки канала при нулевом отклонении верхней стенки от направления потока. Модель SA предсказывает длину отрывной зоны, измеренную в долях высоты
ступеньки, равной 6.1. Она лишь на 2% отличается от экспериментальной величины
6.2H. При угле отклонения 6° модель предсказывает длину циркуляционной зоны в
8.6H, что на 6% отличается от измеренной величины 8.1H.
Таким образом, модель SA является удовлетворительной для многих инженерных приложений. В особенности она применима для расчета обтекания профилей и
крыльев, для которых она была калибрована. В то же время, ее приемлемость для
струйных задач менее убедительна. Показано (1997), что прогнозы коэффициента
расширения осесимметричной затопленной струи по указанной модели вдвое отличаются от данных измерений.
Резюмируя, следует отметить, что рассмотренный класс моделей с одним дифференциальным уравнением обладает большей приемлемостью к описанию турбулентных течений с учетом сжимаемости, переходных явлений, кривизны линий тока
и отрыва потока. Однако объектами их приложения, как правило, являются простые
конфигурации потоков с минимальным набором структурных элементов. Как и в случае алгебраических моделей, сильна привязка к калибровочным типам течений.
Снять указанные ограничения можно, например, при определении масштаба турбулентности как зависимой переменной, т.е. в рамках двух- и многопараметрических
моделей турбулентности.