
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы с использованием производных
|
|
В методах прямого поиска при вычислении значений минимизируемой функции f (x) неизбежно возникают погрешности, к которым чувствительны алгоритмы прямого поиска, основанные на сравнении значений функции в отдельных точках.
Пусть f (x) — дважды непрерывно дифференцируемая функция в окрестности точки x *строгого локального минимума, значения которой вычисляются с абсолютной погрешностью, не превышающей ∆ f. Оценим абсолютную погрешность ∆ *, с которой может быть найдена точка х *с применением метода прямого поиска. Для представления функции f (x) в окрестности точки х *воспользуемся формулой Тейлора с учетом равенства f (x *) = 0:
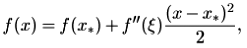
где ξ — точка, лежащая между точками x *и х. Имея в виду, что вычисления проводятся в достаточно малой окрестности точки x *, положим 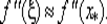 Тогда для приближенно вычисляемых значений
Тогда для приближенно вычисляемых значений 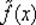 получим
получим
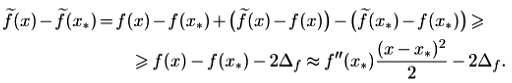
Из этих неравенств вытекает, что можно гарантировать выполнение неравенства 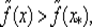 если
если 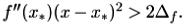 Это приводит к приближенной оценке абсолютной погрешности нахождения точки x *методом прямого поиска:
Это приводит к приближенной оценке абсолютной погрешности нахождения точки x *методом прямого поиска:
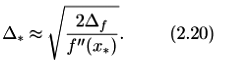
Заданная точность ε *нахождения точки x *не должна быть меньше ∆ *, так как иначе эту точность нельзя достичь методом прямого поиска. Из (2.20) также следует, что при нахождении точки x *происходит потеря примерно половины верных значащих цифр, с которыми можно вычислить приближенное значение минимизируемой функции.
Если унимодальная функция f (x) непрерывно дифференцируема на отрезке минимизации, то точку x *наименьшего значения функции можно вычислять как корень уравнения f '(x) = 0 с помощью тех или иных методов численного решения нелинейных уравнений. В этом случае на точность решения задачи решающее влияние оказывает погрешность вычисления производной функции.
Если абсолютная погрешность вычисления производной не превышает ∆ f ', то для нижней оценки абсолютной погрешности вычисления корня x *уравнения f (x) = 0 имеем
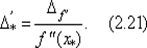
Таким образом, при нахождении этого корня можно сохранить все верные значащие цифры, с которыми можно вычислить значение производной f '(x).
Рассмотрим некоторые методы одномерной минимизации, основанные на использовании производной минимизируемой функции.
Метод средней точки. Будем искать минимум функции f (x), непрерывно дифференцируемой и строго унимодальной на отрезке [ a 1, b 1]. В этом случае единственной точкой x * ∈ [ a 1, b 1] минимума будет стационарная точка, в которой f '(x) = 0. Отметим, что непрерывно дифференцируемая унимодальная на отрезке функция, может иметь на нем более одной стационарной точки.
В методе средней точки используют простую идею: вычисляют производную 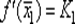 в средней точке
в средней точке 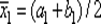 исходного отрезка и, если K 1> 0, то отрезок
исходного отрезка и, если K 1> 0, то отрезок 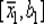 отбрасывают, так как на нем строго унимодальная функция только возрастает, а если K 1< 0. то отбрасывают отрезок
отбрасывают, так как на нем строго унимодальная функция только возрастает, а если K 1< 0. то отбрасывают отрезок 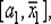 поскольку на нем строго унимодальная функция лишь убывает. В данном случае отбрасывание половины исходного отрезка [ a 1, b 1] аналогично процедуре исключения отрезка. Ясно, что в случае K = 0 имеем
поскольку на нем строго унимодальная функция лишь убывает. В данном случае отбрасывание половины исходного отрезка [ a 1, b 1] аналогично процедуре исключения отрезка. Ясно, что в случае K = 0 имеем 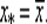
Оставшуюся после отбрасывания половину отрезка обозначим [ a 2, b 2] вычислив производную 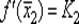 в его средней точке
в его средней точке 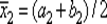 повторим процедуру отбрасывания половины отрезка и т. д. Условием прекращения вычислений на k - м шаге может быть выполнение неравенства lk + 1 < ε *, где lk + 1 = bk + 1 – ak + 1 — длина отрезка [ ak + 1, bk + 1 ] после отбрасывания половины отрезка [ ak, bk ]; ε * — наибольшая допустимая длина интервала неопределенности.
повторим процедуру отбрасывания половины отрезка и т. д. Условием прекращения вычислений на k - м шаге может быть выполнение неравенства lk + 1 < ε *, где lk + 1 = bk + 1 – ak + 1 — длина отрезка [ ak + 1, bk + 1 ] после отбрасывания половины отрезка [ ak, bk ]; ε * — наибольшая допустимая длина интервала неопределенности.
Метод средней точки напоминает метод дихотомии, но сходится к искомому значению x * быстрее, поскольку в отличие от (2.8) для метода средней точки после вычисления п значений производной минимизируемой на отрезке [0, 1] функции f (x) для длины интервала неопределенности получаем
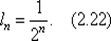
Таким образом, для одинакового уменьшения значения ln в методе средней точки нужно вычислить вдвое меньше значений производной функции по сравнению с числом значений самой функции в методе дихотомии.
Метод Ньютона. Если строго унимодальная на отрезке [ а, b ] функция f (x) дважды непрерывно дифференцируема на этом отрезке, то точку x *∈ [ а, b ] минимума этой функции можно найти путем решения уравнения f '(x) = 0 методом Ньютона, иногда называемым методом касательных. Пусть x 0∈ [ а, b ] — нулевое приближение к искомой точке x *, называемое обычно начальной точкой. Линеаризуем функцию f '(x) в окрестности начальной точки, приближенно заменив дугу графика этой функции касательной в точке (x 0, f '(x 0)):
f '(x) ≈ f '(x 0) + f ''(x 0)(x – x 0). (2.23)
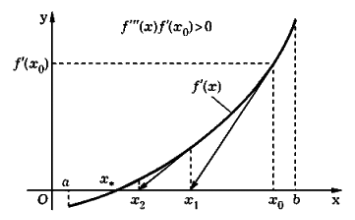
Рис. 2.13
Выберем в качестве следующего приближения к x *точку x 1пересечения касательной с осью абсцисс (рис. 2.13). Приравнивая нулю правую часть (2.23), получаем первый элемент 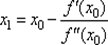 итерационной последовательности { xk }. На { k + 1)-м шаге по найденной на предыдущем шаге точке х k можно найти точку
итерационной последовательности { xk }. На { k + 1)-м шаге по найденной на предыдущем шаге точке х k можно найти точку
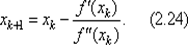
Для квадратичной функции f (x) функция f '(x) линейна. Поэтому в (2.23) равенство будет точным, а метод Ньютона будет сходиться за один шаг при любом выборе точки х 0из области определения этой функции.
· Тема 2. Методы первого порядка