Алгоритмы обобщенного покоординатного спуска на основе конечно-разностных аппроксимаций производных

Достоинством подхода, основанного на применении формул численного дифференцирования, кроме его универсальности, является низкая стоимость подготовки задачи к компьютерному моделированию. От пользователя требуется лишь написание программы для вычисления значения J (x) при заданном х. Реализованные на основе численных производных методы оптимизации оказываются, по существу, прямыми методами, то есть методами, не использующими в своей схеме производные от J. Действительно, заменяя 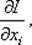например, конечно-разностным отношением 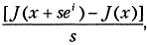где е i = (0,..., 1,..., 0), s ∈ R 1мы фактически используем лишь значения J, вычисленные при определенных значениях аргумента.

Все рассматриваемые нами методы оптимизации строятся на основе использования локальной квадратичной модели минимизируемого функционала, получаемой из общего разложения в ряд Тейлора. Естественно поэтому при выборе формул численного дифференцирования также руководствоваться идеей локальной квадратичной аппроксимации. Исходя иа этого, целесообразно вместо формул с односторонними приращениями применять двусторонние конечно- разностные аппроксимации производных, оказывающиеся точными для квадратичных функционалов. Действительно, легко проверить, что если

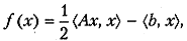
то равенство

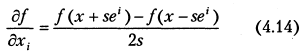
оказывается точным при любом s ≠ 0.

Точно также точным оказывается следующее представление для вторых производных квадратичного функционала

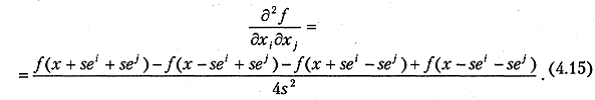
При использовании соотношений (4.14), (4.15) вычислительные затраты характеризуются числом обращений к вычислению значений J (x): для вычисления градиента — 2 n, для вычисления матрицы Гессе — 2 n 2+ 1, где п — размерность вектора х.

Для излагаемых далее методов оптимизации достаточно определять J '(x) и J ''(x) с точностью до множителя, поэтому при реализации формул (4.14), (4.15) деление, соответственно, на 2 s и 4 s 2не производится. Это позволяет избежать известных вычислительных трудностей, если значение s оказывается относительно малым.

В данном случае мы отказываемся от работы с различными шагами s i по отдельным компонентам x i вектора x, предполагая, что последние надлежащим образом нормализованы. В обсуждаемых реализациях метода ОПС шаг дискретности s определяется автоматически в зависимости от величины нормы вектора продвижения || х i – х i – 1|| в пространстве переменных x за один цикл работы алгоритма. Чем большая величина s используется, тем шире предполагаемая область справедливости локальной квадратичной модели исходного функционала. Наибольшая точность вычислений по формуле (4.15) применительно к квадратичным зависимостям достигается при работе с максимально возможным 5, так как в этом случае вклад погрешностей задания значений J в окончательный результат становится наименьшим. Поэтому чем дальше удалось продвинуться на основе построенной квадратичной аппроксимации функционала, то есть чем шире зона ее «полезного действия», тем большие значения s целесообразно выбирать для вычисления производных на следующем этапе поиска. Возможны и другие стратегии регулировки параметра s. Например, сама подпрограмма, реализующая метод оптимизации, может быть настроена на работу с постоянным шагом дискретности. Изменения s в этом случае осуществляются во внешней программе в зависимости от получаемых результатов.

Полученные в результате диагонализации матрицы Гессе новые координатные орты используются далее для реализации базового алгоритма ЦПС с процедурой выбора шагов продвижения по осям, применяемой в алгоритме GZ1. Переход к новым осям координат целесообразно осуществлять после того, как текущие оси «исчерпали себя» и дальнейшего существенного улучшения ситуации не ожидается. В изучаемых алгоритмах обновление осей координат происходит после того, как по каждому из координатных направлений вслед за успешным продвижением последовала неудача в смысле возрастания значения J (х). Укрупненное описание базового алгоритма, реализующего метод ОПС, сводится к следующей последовательности шагов.