Алгоритм SPAC1.

Шаг 1. Ввести исходные данные: x, s.

Шаг 2. Вычислить матрицу В = { b ij }

по формулам

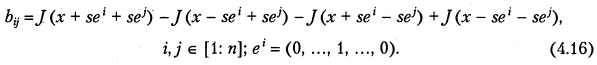
Шаг 3. С помощью процедуры j асо bi построить ортогональную матрицу U, приводящую матрицу В к диагональному виду U T BU.

Шаг 4. В осях { ui }, совпадающих со столбцами матрицы U, реализовать процесс ЦПС (алгоритм GZ1) из точки x до выполнения условия поворота осей; присвоить x полученное лучшее значение, модифицировать s и перейти к шагу 2.

Процесс заканчивается по исчерпании заданного числа обращений к процедуре вычисления J (x). Так же как и в алгоритме GZ1, предусмотрена возможность повторных входов в алгоритм и продолжения вычислений с прерванного места. Приводимые далее результаты работы SPAC1 соответствуют автоматическому выбору шагов дискретности для численного дифференцирования, исходя из равенства

Построенный алгоритм имеет весьма простую структуру, однако его эффективность может быть достаточно высокой, несмотря на необходимость построения матрицы В. В ряде случаев более эффективной оказывается модификация метода ОПС, реализованная в алгоритме SPAC2.

В алгоритме SPAC2 вычисление матрицы вторых производных осуществляется в текущих осях { и i } без возврата к исходному единичному базису { е i }. В результате информация о последнем используемом базисе не теряется, что позволяет сократить трудоемкость решения задачи.

Алгоритм SPAC2 в упрощенном варианте состоит из следующих шагов.