Специальные приемы нормализации

В ряде случаев на уровне аналитического исследования проблемы оптимизации и подготовки ее для компьютерного моделирования удается существенно улучшить структуру задачи с точки зрения ее обусловленности и эффективности последующей процедуры минимизации. Рассмотрим два характерных случая. Первый случай связан с нормализацией некоторой независимой переменной t в задачах аппроксимации по среднестепенным критериям (см. 2.8) и, в частности, по методу наименьших квадратов (МНК). Как правило, переменная t, содержательно трактуемая, например, как частота или время, изменяется в широком диапазоне [ t ', t ''] образуя комбинации с управляемыми параметрами вида 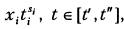где s i может быть достаточно большим. В результате величина 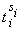оказывается большой, и ее прямое вычисление может привести к переполнению разрядной сетки машины. Соответственно, оптимальное значение x i оказывается сравнимым с нулем (по сути, имеем численный вариант неопределенности типа 0 · ∞. При таких вычислениях, даже при отсутствии аварийных остановов компьютера, катастрофически теряется точность. Проблема снимается, если нормализовать переменную t (а тем самым и все x i) с помощью соотношения t = T τ, = Т > > 1, где τ — новая независимая переменная, 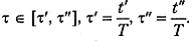Новый управляемый параметр при этом равен 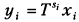и имеет увеличенное в 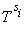раз значение.

Второй случай относится к устранению аддитивных фоновых добавок к целевому функционалу J (x). Если возможно представление J (x) = I (х) + с, с = const, то при достаточно больших абсолютных значениях с необходимо решать задачу минимизации I (х) вместо исходной задачи минимизации J (х). В противном случае могут возникать серьезные вычислительные трудности при построении конечно-разностных аппроксимаций первых и вторых производных J (х). Потеря точности происходит при условии 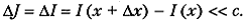Существенно, что общая нормализация значений J (х), согласно п. 2, не изменяет ситуацию к лучшему.