
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод циклического покоординатного спуска
|
|
Решается каноническая задача построения минимизирующей последовательности 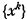 для функционала J (х). Переход от вектора х i к вектору х i +1по методу циклического покоординатного спуска (ЦПС) происходит следующим образом: для l ∈ [1: п ] компонента
для функционала J (х). Переход от вектора х i к вектору х i +1по методу циклического покоординатного спуска (ЦПС) происходит следующим образом: для l ∈ [1: п ] компонента 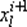 определяется как
определяется как
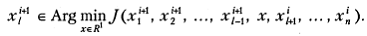
Для плохо обусловленных экстремальных задач этот метод применим в специальных случаях ориентации оврагов вдоль координатных осей. Трудности применения процедур, построенных на основе метода ЦПС, проиллюстрированы на рис. 4.1. Продвижение к точке минимума становится замедленным при наличии вытянутых поверхностей уровня. Как правило, имеет место ситуация «заклинивания», вызываемая дискретным характером представления информации в памяти компьютера.
Множество чисел F в форме с плавающей запятой, которые могут быть представлены в компьютере, конечно и содержит 2(β – 1)β t – 1(М – m + 1) + 1 чисел вида
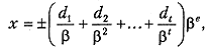
где 0 ≤ di, < β – 1; di — целые числа; β — основание системы исчисления (обычно β = 2), t — длина мантиссы числа; показатель степени е лежит в заданном интервале [ т, М ]. Следовательно, плоскость (x 1, x 2) аппроксимируется также конечным множеством точек, лежащих в узлах сетки, показанной на рис. 4.2.
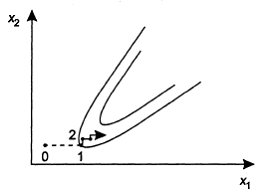
Рис. 4.1. Траектория спуска метода ЦПС при наличии овражной ситуации
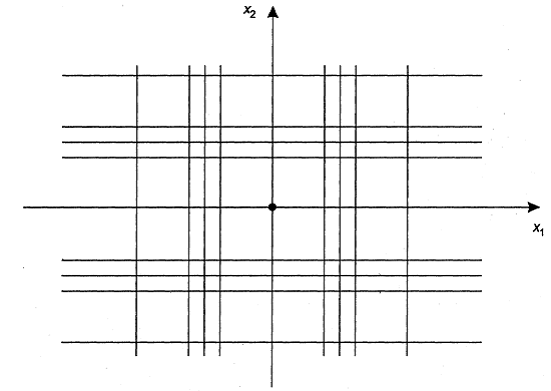
Рис. 4.2. Представление плоскости R 2 в памяти компьютера
Ситуация заклинивания представлена на рис. 4.3. Если процесс попадает в точку A, то ближайшие доступные точки B, В ' и С, С ' соответствуют большему значению функционала. Заклинивание (в англоязычной литературе — jamming) может происходить на значительных расстояниях от точки минимума, приводя к регистрации «ложного» локального минимума. Вероятность заклинивания резко возрастает при использовании негладких функционалов, имеющих минимаксную или максиминную структуру. Типичный случай показан на рис, 4.4.
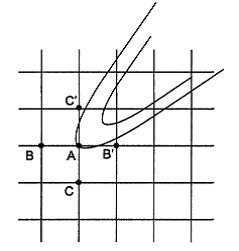
Рис. 4.3. Заклинивание метода ЦПС
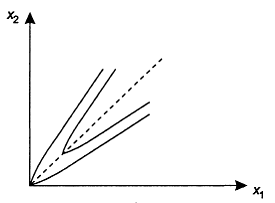
Рис. 4.4. Заклинивание в точке «излома» линии уровня
Несмотря на отмеченную низкую эффективность метода ЦПС в овражной ситуации, его включение в библиотеку алгоритмов целесообразно при решении практически любого класса оптимизационных задач, по крайней мере, как стартового алгоритма с целью получения разумного начального приближения для последующих процедур. Причина этого заключается в высокой надежности метода по отношению к различным сбойным ситуациям, а также в простоте процесса подготовки задачи к моделированию на компьютере. Метод имеет нулевой порядок, то есть не требует включения в вычислительную схему информации о производных от минимизируемого функционала.
При реализации метода могут быть использованы известные из курса численного анализа способы одномерного поиска минимума типа золотого сечения, квадратичной аппроксимации и др. Однако это приводит к заметному и часто неоправданному усложнению алгоритма. Можно привести примеры, когда точный поиск минимума вдоль координатных направлений не только не обязателен, но даже вреден. Поэтому на практике применяются более простые стратегии выбора шагов. Рассмотрим в качестве примера вариант, изложенный в работе.
Задается вектор начальных шагов h = (h 1,..., hn) продвижений из точки х в направлении координатных ортов е 1, е 2,..., е n. Далее шаги hi модифицируются от итерации к итерации. Если выполняется неравенство J (х + hie i) ≤ J (x), то текущая точка x заменяется на х + hie i, а величина hi, утраивается: h i: = 3 h i. После этого осуществляется переход к следующему номеру i. Если J (х + hie i) > J (x), то производится умножение hi на –0, 5 и также осуществляется переход к следующему координатному орту. Таким образом, алгоритм адаптируется к конкретным условиям оптимизации за счет изменения величин и знаков шагов. Если начальные значения шагов были выбраны неудачно, то они быстро скорректируются до необходимых значений.
Указанный метод выбора координатных шагов достаточно эффективен и реализован в алгоритме GZ1. Это, по-видимому, простейшая из возможных реализаций метода ЦПС.
Алгоритм GZ1.
Шаг 1. Ввести начальную точку х = (x 1, …, xn) и шаг s; принять F: =J (x).
Шаг 2. Принять hi: = s, i ∈ [1: п ].
Шаг 3. Принять т: = 1.
Шаг 4. Принять х m: = х m + h m вычислить F 1 = J (х).
Шаг 5. Если F 1≤ F, принять h m: = 3 h m, F: =F 1перейти к шагу 7; иначе — перейти к шагу 6.
Шаг 6. Принять х m: = х m – h m, h m: = –0, 5 h m.
Шаг 7. Принять т: =т + 1. Если т ≤ п, перейти к шагу 4; иначе — к шагу 3.
Выход из алгоритма осуществляется по достижении заданного числа NFM вычислений J. Обычно программа составляется таким образом, чтобы обеспечить возможность продолжения работы с прерванного места после повторных входов в GZ1. В данном случае целесообразно отказаться от применения каких-либо внутренних критериев сходимости процесса оптимизации и обрывать его после заранее обусловленного числа шагов. При необходимости такой анализ сходимости может выполняться во внешней программе путем сравнения результатов, полученных при двух последовательных обращениях к GZ1.
Предполагается, что при каждом новом входе в алгоритм GZ1 счетчик числа вычислений функционала зануляется и, следовательно, разрешается еще NFM обращений к подпрограмме вычисления J (х). Задавая различные значения NFM, можно регулировать частоту выходов из GZ1 во внешнюю программу для оценки и вывода получаемых результатов.