Метод Левенберга

Если известно, что собственные значения матрицы 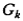расположены в интервале [– т, М ], где М > > m, то можно построить метод, имеющий нелинейную функцию релаксации (рис. 5.4)

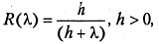(5.22)

удовлетворяющую требованиям (5.7) при ∀ λ ∈ [– т, М ], если h > m.

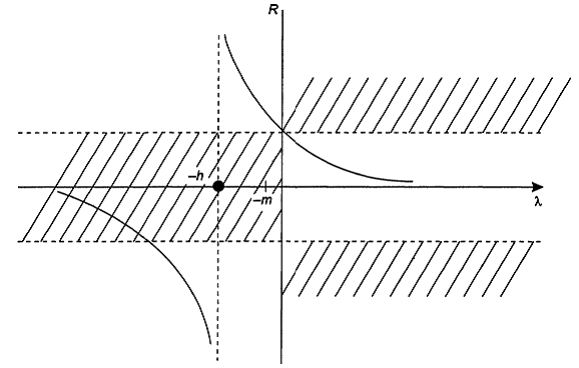
Рис. 5.4. Функция релаксации метода Левенберга

Соответствующий метод предложен Левенбергом для специальных классов оптимизационных задач метода наименьших квадратов и имеет функцию

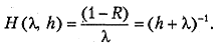(5.23)

Соответствующий метод называется методом Левенберга.

Схема метода (5.2) с функцией (5.23) имеет вид

(5.24)

и реализует некоторый метод доверительной окрестности. Данный метод часто называется также регуляризованным методом Ньютона или методом Маркуардта-Левенберга. Скаляр h на каждом шаге итерационного процесса подбирается так, чтобы матрица 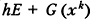была положительно определена и чтобы где величина ∆ может меняться от итерации к итерации.

Реализация метода (5.23) сводится к решению на каждом шаге по k линейной алгебраической системы

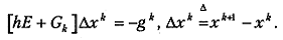(5.25)

Главный недостаток метода заключается в необходимости достаточно точного подбора параметра h, что сопряжено с известными вычислительными трудностями. Значение m, как правило, неизвестно и не может быть вычислено с приемлемой точностью. Лучшее, что обычно можно сделать на практике, — это принять

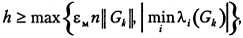(5.26)

где ε м— машинное эпсилон. При этом оценка для т существенно ухудшается при возрастании размерности п. Правая часть неравенства (5.26) обусловлена тем, что абсолютная погрешность представления любого собственного числа матрицы за счет ограниченности разрядной сетки равна

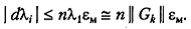
При невыполнении условия h > m система (5.25) может оказаться вырожденной. Кроме этого слева от точки λ = – т функция релаксации быстро входит в запрещенную область, и метод может стать расходящимся. Попытки использования алгоритмического способа более точной локализации h приводят к необходимости многократного решения плохо обусловленной линейной системы (5.25) с различными пробными значениями h.

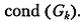Легко видеть, что число обусловленности матрицы может превышать Действительно, потребуем, например, чтобы R (– m) = 10 для обеспечения заданной скорости убывания J (х). Определим необходимую величину параметра h. Имеем 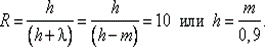В этом случае 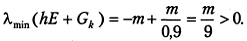Полагая 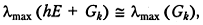получим, что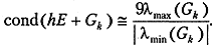

При выборе заведомо больших значений h, что реализуется, например, когда определяющим в (5.26) является первое выражение в скобках, мы имеем m < < h, и величина | R (– m)| ≅ 1, что приводит к медленной сходимости. Ограничение снизу на величину h не позволяет также уменьшить до желаемой величины множители релаксации для λ > 0.

Эти трудности усугубляются при аппроксимации производных конечными разностями, так как при малых значениях 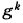для точек , расположенных на дне оврага, мы приходим к необходимости получать компоненты вектора градиента как малые разности относительно больших величин порядка 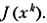В результате компоненты вектора 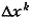будут находиться с большими относительными погрешностями порядка 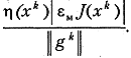Коэффициент овражности η в данном случае и играет роль коэффициента усиления погрешности. Для метода Ньютона справедливо аналогичное замечание. В то же время для метода ПГС точность задания 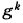может оказаться достаточной для правильного определения направления убывания J (x).