Стратегия поиска

Стратегия метода Флетчера-Ривса [ Fletcher R., Reeves СМ.] состоит в построении последовательности точек { xk }, k = 0, 1,..., таких, что f (xk + 1) < f (xk), k = 0, l,... Точки последовательности { xk } вычисляются по правилу:

Точка х 0задается пользователем, величина шага tk определяется для каждого значения k из условия

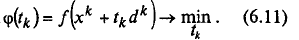
Решение задачи одномерной минимизации (6.11) может осуществляться либо из условия 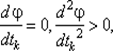либо численно, с использованием методов одномерной минимизации, когда решается задача

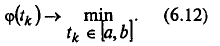
При численном решении задачи определения величины шага степень близости найденного значения tk к оптимальному значению 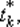удовлетворяющему условиям 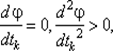зависит от задания интервала [ а, b ] и точности методов одномерной минимизации.

Вычисление величины β k –1по формуле (6.10) обеспечивает для квадратичной формы 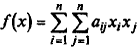построение последовательности Н -сопряженных направлений d 0, d 1,..., dk,..., для которых (dj, Hdi) = 0, ∀ i, j = 0, l,..., k; i ≠ j. При этом в точках последовательности { xk } градиенты функции f (x) взаимно перпендикулярны, т. е.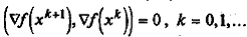

Для квадратичных функций f (x) с матрицей H > 0 метод Флетчера-Ривса является конечным и сходится за число шагов, не превышающее п -размерность вектора х.

При минимизации неквадратичных функций метод не является конечным, при этом следует отметить, что погрешности в решении задачи (6.11) приводят к нарушению не только перпендикулярности градиентов, но и H -сопряженности направлений. Для неквадратичных функций, как правило, используется алгоритм Лолака - Рибьера [ Polak E., Ribiere G.], когда в формулах (6.7)–(6.9) величина β k –1вычисляется следующим образом:

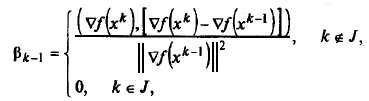
где J = {0, n, 2 n,...}. В отличие от алгоритма Флетчера-Ривса алгоритм Полака-Рибьера предусматривает использование итерации наискорейшего градиентного спуска через каждые n шагов. Построение последовательности { xk } заканчивается в точке, для которой || ∇ f (xk) || < ε 1, где ε 1— заданное число, или при k ≥ М, М — предельное число итераций, или при двукратном одновременном выполнении двух неравенств || xk +1 – xk || < ε 2, | f (xk +1) – f (xk) | < ε 2, где ε 2— малое положительное число.