
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стратегия поиска. Стратегия метода Дэвидона-Флетчера-Пауэлла (Д-Ф-П) [ Davidon W
|
|
Стратегия метода Дэвидона-Флетчера-Пауэлла (Д-Ф-П) [ Davidon W. C., Fletcher R., Powell M. J. D.] состоит в построении последовательности { xk }, k = 0, 1,..., таких, что f (xk + 1) < f (xk), k = 0, l,... Точки последовательности { xk } вычисляются по правилу:
xk + 1 = xk – tkAk ∇ f (xk), k = 0, l,..., (6.13)
где А k есть матрица размера п × п, которая вычисляется по правилу

где 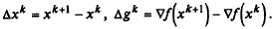
Точка х 0задается пользователем, величина шага tk определяется из условия
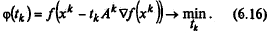
Решение задачи (6.16) может осуществляться как из условий 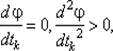 или из условий
или из условий 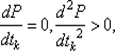 где P (tk) — полином, аппроксимирующий функцию φ (tk), так и численно, т. е. путем поиска решения задачи
где P (tk) — полином, аппроксимирующий функцию φ (tk), так и численно, т. е. путем поиска решения задачи 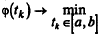 методами одномерной минимизации.
методами одномерной минимизации.
Формулы (6.14), (6.15) при аналитическом решении задачи (6.16) обеспечивают построение последовательности { А k } положительно определенных матриц, таких, что А k → H –1(x *) при k → ∞. Следствием этого для квадратичной функции 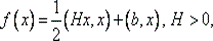 является тот факт, что направления dk, k = 0, 1,..., будут H -сопряженными и, следовательно, алгоритм Д-Ф-П сойдется не более чем за п шагов.
является тот факт, что направления dk, k = 0, 1,..., будут H -сопряженными и, следовательно, алгоритм Д-Ф-П сойдется не более чем за п шагов.
Для неквадратичных функций f (х) алгоритм перестает быть конечным и его сходимость зависит от точности решения задачи (6.16). Глобальную сходимость алгоритма можно гарантировать лишь при его обновлении через каждые п шагов, т. е. когда в формуле (6.13)
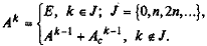
Построение последовательности { х k } заканчивается в точке х k, для которой || ∇ f |(х k)|| < ε 1, где ε 1— заданное число, или при k ≥ М (М — предельное число итераций), или при двукратном одновременном выполнении двух неравенств || xk +1 – xk || < ε 2, | f (xk +1) – f (xk) | < ε 2, где ε 2— малое положительное число.