
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Процедура решения задачи
|
|
1. Используя алгоритм Марквардта, построить точку х k, в которой выполняется по крайней мере один критерий окончания расчетов.
2. Так как f (x) ∈ С 2, то осуществить проверку выполнения достаточных условий минимума H (х k) > 0. Если условие выполнено, то точка х k может рассматриваться как найденное приближение точки минимума х *. Проверку выполнения достаточных условий минимума можно заменить проверкой функции f (x) на выпуклость.
За мечания 7.3.
1. Метод Марквардта за счет выбора μ k обеспечивает построение последовательности { х k }, такой, что f (xk +1) < f (xk), k = 0, 1,...
2. В окрестности точки минимума х *метод Марквардта обладает скоростью сходимости, близкой к квадратичной.
Пример 7.3. Найти локальный минимум функции f (х) = 2 х 12 + х 1 х 2 + х 22.
I. Определение точки х k, в которой выполнен по крайней мере один критерий окончания расчетов.
1 0. Зададим х 0= (0, 5; 1) T, ε 1= 0, 1; М = 10. Найдем градиент функции ∇ f (x) = (4 x 1+ х 2; x 1+ 2 х 2) T и матрицу Гессе 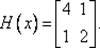
2 0. Положим k = 0, μ 0= 20.
30. Вычислим ∇ f (x 0): ∇ f (x 0) = (3; 2, 5) Т.
40. Проверим выполнение условия || ∇ f (x 0)|| ≤ ε 1: || ∇ f (x 0)|| = 3, 9 > 0, 1. Переходим к шагу 5.
50. Проверим условие k ≥ М: k = 0 < 10. Переходим к шагу 6.
60. Вычислим H (x 0): 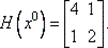
7°. Вычислим Н (х 0) + μ 0 E: Н (х 0) + μ 0 E = 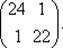
80. Вычислим [ Н (х 0) + μ 0 E ]–1: [ Н (х 0) + μ 0 E ]–1= 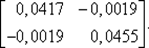
90. Вычислим d 0= – [ Н (х 0) + μ 0 E ]–1∇ f (x 0): d 0= (–0, 119; –0, 108) T.
100.Вычислим х 1= х 0– [ Н (х 0) + μ 0 E ]–1∇ f (x 0): х 1=(0381; 0392) T.
110.Проверим выполнение условия f (x 1) < f (x 0): f (x 1) = 1, 438 < 2 = f (x 0).
120.Полагаем 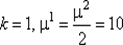 и переходим к шагу 3.
и переходим к шагу 3.
31. Вычислим ∇ f (x 1): ∇ f (x 1) = (2, 41; 2, 16) T.
41. Проверим выполнение условия || ∇ f (x 1) || ≤ ε 1: || ∇ f (x 1) || = 3, 18 > 0, 1. Переходим к шагу 5.
51. Проверим выполнение условия k ≥ М: k = 1 < 10. Переходим к шагу 6.
61. Вычислим Н (х 1): 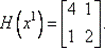
71. Вычислим Н (х 1) + μ 1 E:
Н (х 1) + μ 1 E = 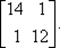
81. Вычислим [ Н (х 1) + μ 1 E ]–1:
[ Н (х 1) + μ 1 E ]–1= 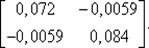
91. Вычислим d 1= – [ Н (х 1) + μ 1 E ]–1∇ f (x 1): d 1= (–0, 160; –0, 168) T.
101. Вычислим х 2= х 1– [ Н (х 1) + μ 1 E ]–1∇ f (x 1):
х 2= (0, 381; 0, 892) T – (0, 160; 0, 168) T = (0, 221; 0, 724) T.
111. Проверим выполнение условия f (x 2) < f (x 1):
f (x 2) = 0, 791 < 1, 438 = f (x 1).
121. Полагаем 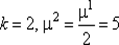 и переходим к шагу 3.
и переходим к шагу 3.
32. Вычислим ∇ f (x 2): ∇ f (x 2) = (1, 60; 1, 67) T.
42. Проверим выполнение условия || ∇ f (x 2) || ≤ ε 1: || ∇ f (x 2) || = 2, 31 > 0, l. Переходим к шагу 5.
52. Проверим выполнение условия k ≥ М: k = 2 < 10. Переходим к шагу 6.
62. Вычислим Н (х 2): 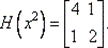
72. Вычислим Н (х 2) + μ 2 E:
Н (х 2) + μ 2 E = 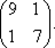
82. Вычислим [ Н (х 2) + μ 2 E ]–1:
[ Н (х 2) + μ 2 E ]–1= 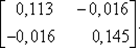
92. Вычислим d 2= – [ Н (х 2) + μ 2 E ]–1∇ f (x 2): d 2= (–0, 155; –0, 217) T.
102. Вычислим х 3 = х 2– [ Н (х 2) + μ 2 E ]–1∇ f (x 2):
х 3= (0, 221; 0, 724) T – (0, 155; 0, 217) T = (0, 07; 0, 51) T.
112. Проверим выполнение условия f (x 3) < f (x 2):
f (x 3) = 0, 3 < 0, 791 = f (x 2).
122. Полагаем 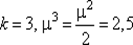 и переходим к шагу 3.
и переходим к шагу 3.
33. Вычислим ∇ f (x 3): ∇ f (x 3) = (0, 79; 1, 09) T.
43. Проверим выполнение условия || ∇ f (x 3) || ≤ ε 1: || ∇ f (x 3) || = l, 34 > 0, l. Переходим к шагу 5.
53. Проверим выполнение условия k ≥ М: k = 3 < 10. Переходим к шагу 6.
63. Вычислим Н (х 3): 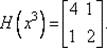
73. Вычислим Н (х 3) + μ 3 E:
Н (х 3) + μ 3 E = 
83. Вычислим [ Н (х 3) + μ 3 E ]–1:
[ Н (х 3) + μ 3 E ]–1= 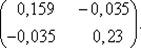
93. Вычислим d 3= – [ Н (х 3) + μ 3 E ]–1∇ f (x 3): d 3= (–0, 078; –0, 22) T.
103. Вычислим х 4 = х 3– [ Н (х 3) + μ 3 E ]–1∇ f (x 3):
х 4= (0, 07; 0, 51) T – (0, 078; 0, 22) T = (–0, 008; 0, 29) T.
113. Проверим выполнение условия f (x 4) < f (x 3):
f (x 4) = 0, 082 < 0, 3 = f (x 3).
123. Полагаем 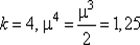 и переходим к шагу 3.
и переходим к шагу 3.
34. Вычислим ∇ f (x 4): ∇ f (x 4) = (0, 26; 0, 57) T.
44. Проверим выполнение условия || ∇ f (x 4) || ≤ ε 1: || ∇ f (x 4) || = 0, 62 > 0, l. Переходим к шагу 5.
54. Проверим выполнение условия k ≥ М: k = 4 < 10. Переходим к шагу 6.
64. Вычислим Н (х 4): 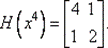
74. Вычислим Н (х 4) + μ 4 E:
Н (х 4) + μ 4 E = 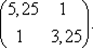
84. Вычислим [ Н (х 4) + μ 4 E ]–1:
[ Н (х 4) + μ 4 E ]–1= 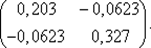
94. Вычислим d 4= – [ Н (х 4) + μ 4 E ]–1∇ f (x 4): d 4= (–0, 017; –0, 17) T.
104. Вычислим х 5 = х 4– [ Н (х 4) + μ 4 E ]–1∇ f (x 4):
х 5= (–0, 008; 0, 29) T – (0, 017; 0, 17) T = (0, 025; 0, 12) T.
114. Проверим выполнение условия f (x 5) < f (x 4):
f (x 5) = 0, 012 < 0, 082 = f (x 4).
124. Полагаем 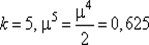 и переходим к шагу 3.
и переходим к шагу 3.
35. Вычислим ∇ f (x 5): ∇ f (x 5) = (0, 02; 0, 22) T.
45. Проверим выполнение условия || ∇ f (x 5) || ≤ ε 1: || ∇ f (x 5) || = 0, 22 > 0, l. Переходим к шагу 5.
55. Проверим выполнение условия k ≥ М: k = 5 < 10. Переходим к шагу 6.
65. Вычислим Н (х 5): 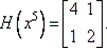
75. Вычислим Н (х 5) + μ 5 E:
Н (х 5) + μ 5 E = 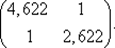
85. Вычислим [ Н (х 5) + μ 5 E ]–1:
[ Н (х 5) + μ 5 E ]–1= 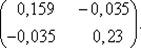
95. Вычислим d 5= – [ Н (х 5) + μ 5 E ]–1∇ f (x 5): d 5= (–0, 015; –0, 090) T.
105. Вычислим х 6 = х 5– [ Н (х 5) + μ 5 E ]–1∇ f (x 5):
х 6= (0, 025; 0, 12) T – (0, 015; –0, 09) T = (–0, 01; 0, 03) T.
115. Проверим выполнение условия f (x 6) < f (x 5):
f (x 6) = 0, 0006 < 0, 012 = f (x 5).
125. Полагаем 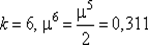 и переходим к шагу 3.
и переходим к шагу 3.
36. Вычислим ∇ f (x 6): ∇ f (x 6) = (–0, 01; 0, 05) T.
46. Проверим выполнение условия || ∇ f (x 6) || ≤ ε 1: || ∇ f (x 6) || = 0, 051 < 0, l. Расчет окончен.
II. Анализ точки х 1.
Точка х 6= (–0, 01; 0, 03) T (рис. 7.2) является найденным приближением точки минимума x *, так как функция f (х) = 2 х 12+ х 1 х 2+ х 22 является строго выпуклой (см. пример 7.1). На рис. 7.2 полученная траектория спуска изображена пунктирной линией.
· Тема 4. Численные методы поиска условного экстремума
·