Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стратегия поиска. Для ограничений типа равенств применяется метод штрафов (внешних штрафов), а для ограничений-неравенств — метод барьерных функций (внутренних штрафов).
|
|
Для ограничений типа равенств применяется метод штрафов (внешних штрафов), а для ограничений-неравенств — метод барьерных функций (внутренних штрафов).
Задача на условный минимум сводится к решению последовательности задач поиска минимума смешанной вспомогательной функции:
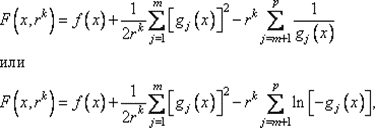
где rk ≥ 0 — параметр штрафа.
Начальная точка задается так, чтобы ограничения-неравенства строго выполнялись: gj (x) < 0, j = m + 1,..., p. На каждой k - й итерации ищется точка x *(rk)минимума смешанной вспомогательной функции при заданном параметре rk с помощью одного из методов безусловной минимизации. Полученная точка x *(rk) используется в качестве начальной на следующей итерации, выполняемой при уменьшающемся значении параметра штрафа. При rk → +0 последовательность точек x *(rk) стремится к точке условного минимума x *.
Алгоритм
Шаг 1. Задать начальную точку х 0так, чтобы gj (x) < 0, j = m + 1,..., p; начальное значение параметра штрафа r 0 > 0; число С > 1 для уменьшения параметра штрафа; малое число ε для остановки алгоритма. Положить k = 0.
Шаг 2. Составить смешанную вспомогательную функцию
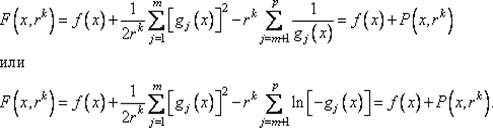
Шаг 3. Найти точку x *(rk) минимума функции F (x *, rk) с помощью какого-либо метода поиска безусловного минимума с проверкой выполнения справедливости неравенств: gj (x) < 0, j = m + 1,..., p. При этом задать все требуемые выбранным методом параметры. В качестве начальной точки взять х k.
Шаг 4. Вычислить P (х *(rk), rk) и проверить условие окончания:
а) если | P (х *(rk), rk) | ≤ ε, процесс поиска закончить:
х *= x *(rk), f (х *) = f (x *(rk));
б) если | P (х *(rk), rk) | > ε, положить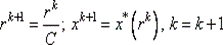 
и перейти к шагу 2.