
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод барьерных функций
|
|
Постановка задачи
Даны дважды непрерывно дифференцируемые целевая функция f (x) = f (x 1,.., xn) и функции ограничений-неравенств gj (x) ≤ 0, j = 1,..., m, определяющие множество допустимых решений X.
Требуется найти локальный минимум целевой функции на множестве X, т. е. такую точку х *∈ X, что
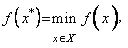
где X = { x | gj (x) ≤ 0, j = 1,..., m }.
Стратегия поиска
Идея метода заключается в сведении задачи на условный минимум к решению последовательности задач поиска минимума вспомогательной функции F (x, rk) = f (x) + P (x, rk), где P (x, rk) — штрафная функция, rk > 0 — параметр штрафа.
Как правило, используются:
а) обратная штрафная функция 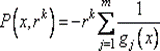 (рис. 9.7, а);
(рис. 9.7, а);
б) логарифмическая штрафная функция 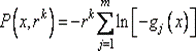 (рис. 9.7, б).
(рис. 9.7, б).
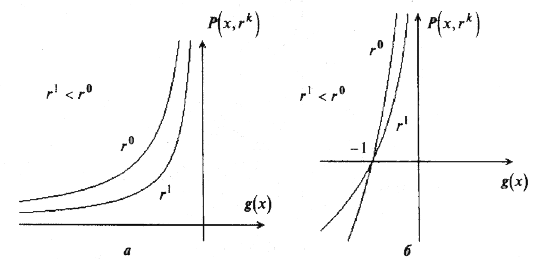
Рис 9.7
Обе штрафные функции определены и непрерывны внутри множества Х, т. е. на множестве { x | gj (x) < 0, j = 1,..., m }, и стремятся к бесконечности при приближении к границе множества изнутри. Поэтому они называются барьерными функциями. При rk > 0 штрафная функция, задаваемая обратной функцией, положительна. Логарифмическая штрафная функция положительна при –1 < g (x) < 0 и отрицательна при g (x) < –1, т. е. внутренним точкам области отдается предпочтение перед граничными точками.
Начальная точка задается только внутри множества X. На каждой k - й итерации ищется точка x *(rk) минимума вспомогательной функции F (x, rk) при заданном параметре rk с помощью одного из методов безусловной минимизации. Полученная точка x *(rk) используется в качестве начальной на следующей итерации, выполняемой при уменьшающемся значении параметра штрафа. При rk → +0 последовательность точек x *(rk) стремится к точке условного минимума х *. Барьерные функции как бы препятствуют выходу из множества X, а если решение задачи лежит на границе, то процедура метода приводит к движению изнутри области к границе.
Заметим, что согласно описанной процедуре точки x *(rk) лежат внутри множества допустимых решений для каждого rk. Этим объясняется то, что метод барьерных функций иногда называется методом внутренних штрафов.
Алгоритм
Шаг 1. Задать начальную точку х 0внутри области X; начальное значение параметра штрафа rk ≥ 0; число С > 1 для уменьшения параметра штрафа; малое число ε > 0 для остановки алгоритма. Положить k = 0.
Шаг 2. Составить вспомогательную функцию:
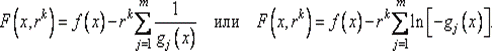
Шаг 3. Найти точку x *(rk) минимума функции F (x, rk) с помощью какого-либо метода (нулевого, первого или второго порядка) поиска безусловного минимума с проверкой принадлежности текущей точки внутренности множества X. При этом задать все требуемые выбранным методом параметры. В качестве начальной точки взять х k. Вычислить:
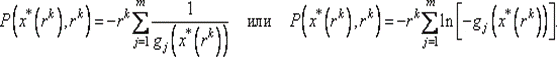
Шаг 4. Проверить выполнение условия окончания:
а) если | P (х *(rk), rk) | ≤ ε, процесс поиска закончить: х *= x *(rk), f (х *) = f (x *(rk));
б) если | P (х *(rk), rk) | > ε, положить 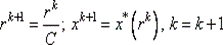 и перейти к шагу 2.
и перейти к шагу 2.