
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стратегия поиска. Идея метода заключается в сведении задачи на условный минимум к решению последовательности задач поиска безусловного минимума вспомогательной функции :
|
|
Идея метода заключается в сведении задачи на условный минимум к решению последовательности задач поиска безусловного минимума вспомогательной функции:
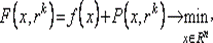
где P (x, rk) — штрафная функция, rk — параметр штрафа, задаваемый на каждой k -й итерации. Это связано с возможностью применения эффективных и надежных методов поиска безусловного экстремума... Штрафные функции конструируются, исходя из условий:

причем при невыполнении ограничений и rk → ∞, k → ∞ справедливо P (x, rk) → ∞. Чем больше rk, тем больше штраф за невыполнение ограничений. Как правило, для ограничений типа равенств используется квадратичный штраф (рис. 9.1, а), а для ограничений типа неравенств — квадрат срезки (рис. 9.1, б):
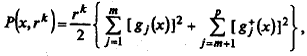
где 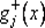 — срезка функции:
— срезка функции:
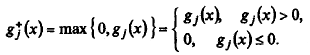
Начальная точка поиска задается обычно вне множества допустимых решений X. На каждой k - й итерации ищется точка x *(rk) минимума вспомогательной функции F (x, rk) при заданном параметре rk с помощью одного из методов безусловной минимизации. Полученная точка x *(rk) используется в качестве начальной на следующей итерации, выполняемой при возрастающем значении параметра штрафа. При неограниченном возрастании rk последовательность точек x *(rk) стремится к точке условного минимума х *.

Рис. 9.1
Алгоритм
Шаг 1. Задать начальную точку х 0; начальное значение параметра штрафа r 0> 0; число С > 1 для увеличения параметра; малое число ε > 0 для остановки алгоритма. Положить k = 0.
Шаг 2. Составить вспомогательную функцию
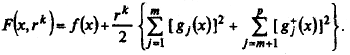
Шаг 3. Найти точку x *(rk) безусловного минимума функции F (x, rk) по x с помощью какого-либо метода (нулевого, первого или второго порядка):
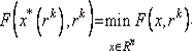
При этом задать все требуемые выбранным методом параметры. В качестве начальной точки взять х k. Вычислить P (x *(rk), rk).
Шаг 4. Проверить условие окончания:
а) если P (x *(rk), rk) ≤ ε, процесс поиска закончить:
x *= x *(rk), f (x *) = f (x *(rk));
б) если P (x *(rk), rk) > ε, положить: rk + 1 = C rk, xk + l= x *(rk), k = k + 1 и перейти к шагу 2.