Стратегия поиска. Стратегия метода Ньютона [ Newton I .] состоит в построении последовательности точек { xk}, k = 0, 1

Стратегия метода Ньютона [ Newton I.] состоит в построении последовательности точек { xk }, k = 0, 1,..., таких, что f (xk + 1) < f (xk), k = 0, l,... Точки последовательности вычисляются по правилу

xk + 1 = xk + dk, k = 0, 1,..., (7.1)

где х 0— задается пользователем, а направление спуска dk определяется для каждого значения k по формуле

dk = – H –1(xk) ∇ f (xk). (7.2)

Выбор dk по формуле (7.2) гарантирует выполнение требования f (xk + 1) < f (xk) при условии, что H (xk) > 0. Формула (7.2) получена из следующих соображений:

1. Функция f (x) аппроксимируется в каждой точке последовательности { xk } квадратичной функцией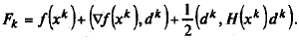

2. Направление dk определяется из необходимого условия экстремума первого порядка: 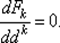Таким образом, при выполнении требования H (xk) > 0 последовательность является последовательностью точек минимумов квадратичных функций Fk, k = 0, 1,... (рис. 7.1). Чтобы обеспечить выполнение требования f (xk + 1) < f (xk), k = 0, l,..., даже в тех случаях, когда для каких-либо значений матрица Гессе H (xk) не окажется положительно определенной, рекомендуется для соответствующих значений k вычислить точку xk + 1 по методу градиентного спуска xk + 1 = xk – tk ∇ f (xk) с выбором величины шага tk из условия f (xk – tk ∇ f (xk)) < f (xk).

Построение последовательности { х k } заканчивается в точке х k, для которой || ∇ f (xk) || < ε 1, где ε 1— заданное малое положительное число, или при k ≥ М (M — предельное число итераций), или при двукратном, одновременном выполнении двух неравенств || xk +1 – xk || < ε 2, | f (xk +1) – f (xk) | < ε 2, где ε 2— малое положительное число. Вопрос о том, может ли точка х k рассматриваться как найденное приближение искомой точки минимума, решается путем проведения дополнительного исследования, которое описано ниже.

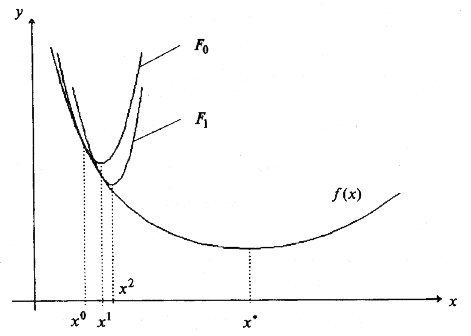
Рис. 7.1