Процедура решения задачи. 1. Используя алгоритм Ньютона, найти точку х k, в которой выполняется по крайней мере один критерий окончания расчета.

1. Используя алгоритм Ньютона, найти точку х k, в которой выполняется по крайней мере один критерий окончания расчета.

2. Так как f (х) ∈ С 2, то осуществить проверку выполнения достаточных условий минимума H (х k) > 0. Если условие выполнено, то точка х k может рассматриваться как найденное приближение точки минимума х *. Проверку выполнения достаточных условий минимума можно заменить проверкой функции f (х) на выпуклость.

Пример 7.1. Найти локальный минимум функции

f (х) = 2 х 12 + х 1 х 2 + х 22.

I. Определение точки х k, в которой выполнен по крайней мере один из критериев окончания расчетов.

1. Зададим х 0, ε 1, ε 2, М: х 0= (0, 5; 1) T, ε 1= 0, 1; ε 2= 0, 15; М = 10. Найдем градиент функции ∇ f (x) = (4 x 1+ х 2; x 1+ 2 х 2) T и матрицу Гессе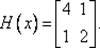

2. Положим k = 0.

30. Вычислим ∇ f (x 0): ∇ f (x 0) = (3; 2, 5) Т.

40. Проверим выполнение условия || ∇ f (x 0)|| ≤ ε 1: || ∇ f (x 0)|| = 3, 9 > 0, 1. Переходим к шагу 5.

50. Проверим условие k ≥ М: k = 0 < 10. Переходим к шагу 6.

60. Вычислим H (x 0):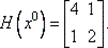

7 0. Вычислим H –1(x 0):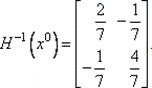

80. Проверим выполнение условия H –1(x 0) > 0. Так как 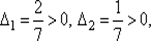то согласно критерию Сильвестра H –1(x 0) > 0.

90. Определим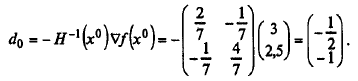

100. Вычислим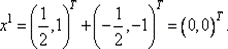

110. Проверим выполнение условий || x 1 – x 0|| < ε 2, | f (x 1) – f (x 0) | < ε 2

|| x 1 – x 0|| = 1, 12 > 0, 15; | f (x 1) – f (x 0) | = 2 > 0, 15.

Полагаем k = 1, переходим к шагу 3.

31. Вычислим ∇ f (x 1): ∇ f (x 1) = (0, 0) T.

41. Проверим выполнение условия || ∇ f (x 1)|| < ε 1: || ∇ f (x 1)|| = 0< 0, 1. Расчет

окончен. Заметим, что в точке х 1выполняется необходимое условие первого порядка, поэтому она является стационарной точкой.

II. Анализ точки х 1.

Функция f (х) = 2 x 12+ x 1 x 2+ х 22является строго выпуклой, так как ее матрица вторых производных 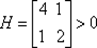в силу того, что ∆ 1= 4 > 0, ∆ 2=7 > 0. Найденная точка х 1= (0, 0) T есть точка локального и одновременно глобального минимума f (x).

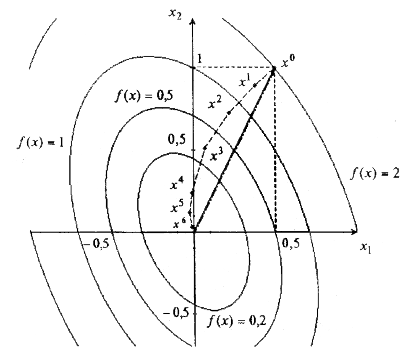
Рис. 7.2

На рис. 7.2 траектория спуска изображена сплошной линией.