Алгоритм. Шаг 1. Задать х 00, ε1>0, ε2>0; предельное число М циклов счета, кратное n , где n — размерность вектора х

Шаг 1. Задать х 00, ε 1> 0, ε 2> 0; предельное число М циклов счета, кратное n, где n — размерность вектора х. Найти градиент ∇ f (x).

Шаг 2. Задать номер цикла j = 0.

Шаг 3. Проверить условие j > М:

а) если j ≥ М, то расчет окончен и х *= х jk;

б) если j < М, то перейти к шагу 4.

Шаг 4. Задать k = 0.

Шаг 5. Проверить условие k ≤ п – 1:

а) если k ≤ п – 1, то перейти к шагу 6;

б) если k = п, то положить j = j + 1 и перейти к шагу 3.

Шаг 6. Вычислить ∇ f (х jk).

Шаг 7. Проверить выполнение условия || ∇ f (xjk)|| < ε 1:

а) если условие выполнено, то расчет окончен и х *= xjk;

б) если нет, то перейти к шагу 8.

Шаг 8. Вычислить t * k из условия

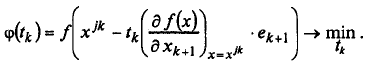
Шаг 9. Вычислить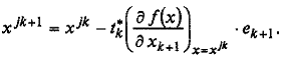

Шаг 10. Проверить выполнение условий

|| xjk +1 – xjk || < ε 2, || f (xjk +1) – f (xjk) || < ε 2:

а) если оба условия выполнены в двух последовательных циклах с номерами j и j – 1, то расчет окончен, найдена точка х *= xjk +1;

б) если не выполняется хотя бы одно условие, положить k = k +1 и перейти к шагу 5.

Геометрическая интерпретация метода для п = 2 приведена на рис. 6.6.

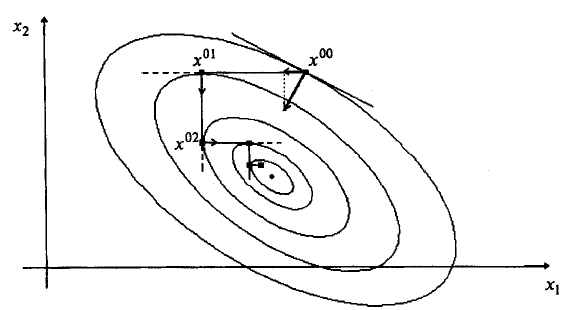
Рис. 6.6

Пример 6.4. Найти локальный минимум функции

f (х) = 2 х 12+ х 1 х 2+ х 22.

I. Определение точки xjk, в которой выполнен хотя бы один из критериев окончания расчетов.

1. Зададим х 00, ε 1, ε 2, M: х 00=(0, 5; 1) T, ε 1= 0, 1; ε 2= 0, 15; М = 10. Найдем градиент функции в произвольной точке ∇ f (х) = (4 x 1+ x 2; x 1+ 2х2) T.

2. Зададим j = 0.

3. Проверим выполнение условия j ≥ M: j = 0 < 10 = М.

4. Зададим k = 0.

5. Проверим выполнение условия к ≤ п – 1: k = 0 < 1 = п – 1.

6. Вычислим ∇ f (х 00): ∇ f (х 00) = (3; 2, 5) Т.

7. Проверим условие || ∇ f (х 00)|| < ε 1,: || ∇ f (х 00)|| = 3, 9 > 0, 1.

8. Определим величину шага 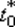из условия

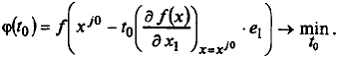
Воспользуемся формулой (6.6) при k = 0, j = 0: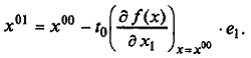

Поскольку 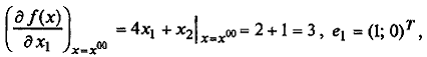, то

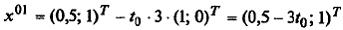или 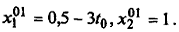Подставляя полученные выражения в f (х), имеем φ (t 0) = 2(0, 5 – 3 t 0)2+ (0, 5 – 3 t 0) · 1 +1.

Из необходимого условия экстремума 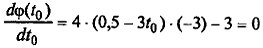или 36 t 0 – 9 = 0 находим Так как 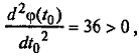то найденное значение шага обеспечивает минимум функции φ (t 0) по t 0.