Стратегия поиска. Стратегия метода Гаусса-Зейделя [ Gauss - Seidel ] состоит в построении последовательности точек { xk}

Стратегия метода Гаусса-Зейделя [ Gauss - Seidel ] состоит в построении последовательности точек { xk }, k = 0, 1,..., таких, что f (xk + 1) < f (xk), k = 0, l,...

Точки последовательности { xk } вычисляются по правилу

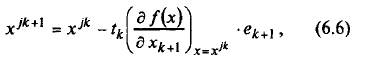
где j — номер цикла вычислений, j = 0, 1, 2,...; k — номер итерации внутри цикла, k = 0, 1,..., n – 1; е k + 1 — единичный вектор, (k + 1) - я проекция которого равна 1; точка x 00задается пользователем, величина шага tk выбирается из условия

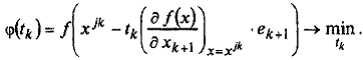
Эта задача является задачей одномерной минимизации функции 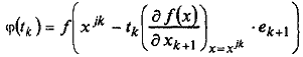и может быть решена либо с использованием условий 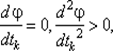либо численно с использованием методов одномерной минимизации, как задача .

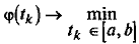Если уравнение 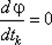имеет высокую степень и корни его трудно определить, можно аппроксимировать функцию φ (tk) полиномом P (tk) второй или третьей степени и определить t * k из условий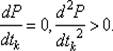

При численном решении задачи определения величины шага степень близости найденного значения tk к оптимальному значению t * k, удовлетворяющему условиям 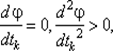зависит от задания интервала [ а, b ] и точности методов одномерной минимизации.

Легко видеть, что при фиксированном j за одну итерацию с номером k изменяется только одна проекция точки х jk, имеющая номер k + 1, а в течение всего цикла с номером j, т. е. начиная с k = 0 и кончая k = n – 1, изменяются все п проекций точки х j 0. После этого точке х jn присваивается номер х j +1, 0и она берется за начальную точку для вычислений в (j + 1)-м цикле.

Расчет заканчивается в точке xjk при выполнении по крайней мере одного из трех критериев окончания счета: || ∇ f (xjk)|| < ε 1, или k ≥ М, или двукратного выполнения неравенств 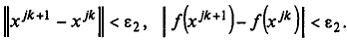Здесь ε 1, ε 2— малые положительные числа, М — предельное число циклов итераций.

Полученные в результате вычислений точки могут быть записаны как элементы последовательности { х l }, где l = n · j + k — порядковый номер точки, т. е. { х l } = { x 0= x 00, x 1= x 01, …, xn = x 0 n = x 10, xn + 1 = x 11, xn + 2 = x 12, …}.