Алгоритм

Шаг 1. Задать x 0, ε 1> 0, ε 2> 0, M — предельное число итераций. Найти ∇ f (x).

Шаг 2. Положить k = 0.

Шаг 3. Вычислить ∇ f (xk).

Шаг 4. Проверить выполнение критерия окончания || ∇ f (xk) || < ε 1:

а) если критерий выполняется, х *= х k, расчет окончен;

б) если нет, то перейти к шагу 5.

Шаг 5. Проверить условие k ≥ М:

а) если неравенство выполняется, то расчет окончен и х *= х k

Шаг 6. Определить d 0= – ∇ f (x 0).

Шаг 7. Определить

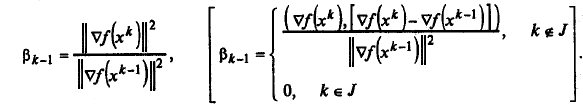
Шаг 8. Определить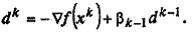

Шаг 9. Найти 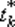из условия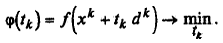

Шаг 10. Вычислить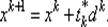

Шаг 11. Проверить выполнение условий

|| xk +1 – xk || < ε 2, | f (xk +1) – f (xk) | < ε 2:

а) в случае выполнения обоих условий в двух последовательных итерациях с номерами к и к - 1 расчет окончен, найдена точка х *= х k + 1;

б) если не выполняется хотя бы одно из условий, полагаем k = k + 1 и переходим к шагу 3.

Геометрическая интерпретация метода для n = 2 изображена на рис. 6.7.

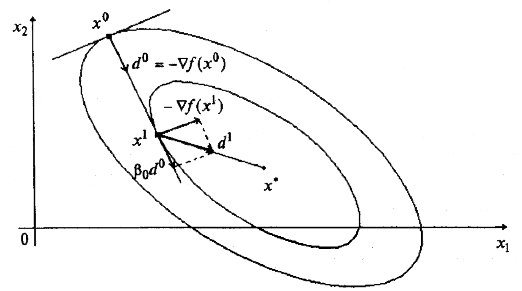
Рис. 6.7

Пример 6.5. Найти локальный минимум функции f (х) = 2 х 12 + х 1 х 2 + х 22.

I. Определение точки х k, в которой выполнен по крайней мере один из критериев окончания расчетов.

1. Зададим х 0, ε 1, ε 2, М: х 0= (0, 5; 1) T, ε 1= 0, 1; ε 2= 0, 15; М = 10. Найдем градиент функции в произвольной точке ∇ f (x) = (4 x 1+ х 2; x 1+ 2 х 2) T.

2. Положим k = 0.

30. Вычислим ∇ f (x 0): ∇ f (x 0) = (3; 2, 5) Т.

40. Проверим условие || ∇ f (x 0)|| < ε 1: || ∇ f (x 0)|| = 3, 9 > 0, 1.

50. Проверим условие k ≥ М: k = 0 < 10 = M.

6°. Определим d 0= – ∇ f (x 0): d 0= –(3; 2, 5) T.

90. Определим 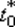из условия .

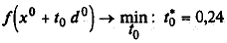100. Вычислим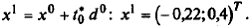

110. Проверим условия || x 1– x 0|| < ε 2, | f (x 1) – f (x 0)| < ε 2:

|| x 1– x 0|| = 0, 937 > 0, 15; | f (x 1) – f (x 0)| = |0, 17 – 2| = 1, 83 > 0, 15.

Полагаем k = 1, переходим к шагу 3.

31. Вычислим ∇ f (x 1): ∇ f (x 1) = (–0, 48; 0, 58) T.

41. Проверим условие || ∇ f (x 1)|| < ε 1: || ∇ f (x 1)|| = 0, 752 > 0, 1.

51. Проверим условие k ≥ М: k = 1 < 10 = М.

71. Определим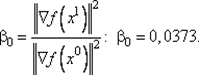

81. Определим d l= – ∇ f (x 0)+ β 0 d 0:

d 1= –(–0, 48; 0, 58) T – 0, 0373 (3; 2, 5) T = (0, 368; –0, 673) T.

91. Определим 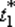из условия 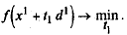Воспользуемся формулой

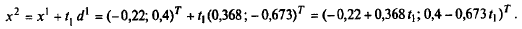
Подставляя полученное выражение в f (х), имеем

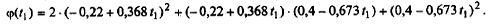
Применяя необходимое условие безусловного экстремума

находим 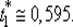Поскольку 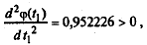найденное значение шага обеспечивает минимум функции φ (t 1) по t 1.

10 l. Вычислим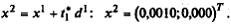

111. Проверим условия || x 2– x 1|| < ε 2, | f (x 2) – f (x 1)| < ε 2:

|| x 2– x 1|| = 0, 456 > 0, 15; | f (x 2) – f (x 1)| = 0, 17 > 0, 15.

Полагаем k = 2 и переходим к шагу 3.

32. Вычислим ∇ f (x 2): ∇ f (x 2) = (0, 003; 0, 006) T.

42. Проверим условие || ∇ f (x 2)|| < ε 1: || ∇ f (x 2)|| = 0, 0067 < 0, 1. Расчет окончен. Найдена точка х 2= (0, 001; 0) T; f (x 2) = 2 · 10–6. На рис. 6.8 полученные точки соединены пунктирной линией.

II. Анализ точки х 2.

Функция f (х) = 2 х 12+ х 1 х 2+ х 22есть квадратичная функция двух переменных, имеющая положительно определенную матрицу вторых производных 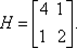Это позволяет сделать вывод о том, что функция f (х) строго выпукла, следовательно, имеет единственный минимум, приближение которого х 2= (0, 001; 0) T найдено за две итерации.

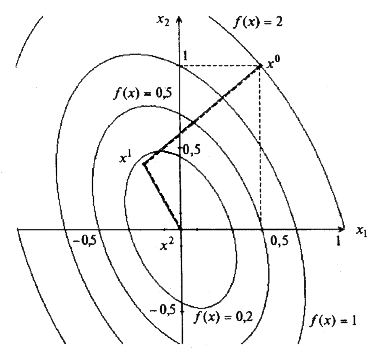
Рис. 6.8