
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дискретные случайные величины. Определение 13.1. Случайная величина Х называется дискретной, если она принимает конечное либо счётное число значений.
|
|
Определение 13.1. Случайная величина Х называется дискретной, если она принимает конечное либо счётное число значений.
Определение 13.2. Законом распределения случайной величины Х называется совокупность пар чисел (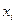 ,
, 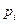 ), где
), где 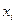 – возможные значения случайной величины, а
– возможные значения случайной величины, а 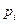 – вероятности, с которыми случайная величина принимает эти значения, т.е.
– вероятности, с которыми случайная величина принимает эти значения, т.е. 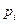 = P{ X =
= P{ X = 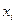 }, причём
}, причём 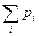 =1.
=1.
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности. Такая таблица называется рядом распределения дискретной случайной величины.
| Х | 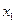
| 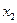
| … | 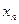
| … |
| Р | 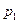
| 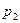
| … | 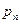
| … |
Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывается 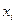 , по оси ординат – вероятность
, по оси ординат – вероятность 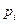 . Точки с координатами (
. Точки с координатами (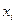 ,
, 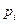 ) соединяют отрезками и получают ломаную, называемую многоугольником распределения, который является одной из форм задания закона распределения дискретной случайной величины.
) соединяют отрезками и получают ломаную, называемую многоугольником распределения, который является одной из форм задания закона распределения дискретной случайной величины.
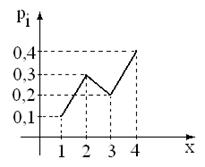 Пример 13.3. Построить многоугольник распределения случайной величины Х с рядом распределения
Пример 13.3. Построить многоугольник распределения случайной величины Х с рядом распределения
| Х | ||||
| Р | 0, 1 | 0, 3 | 0, 2 | 0, 4 |
Определение 13.4. Говорят, что дискретная случайная величина Х имеет биноминальное распределение с параметрами (n, p)если она может принимать целые неотрицательные значения k 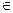 {1, 2, …, n } с вероятностями Р(Х=х)=
{1, 2, …, n } с вероятностями Р(Х=х)= 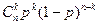 .
.
Ряд распределения имеет вид:
| Х | … | k | … | n | ||
| Р | 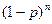
| 
| … | 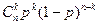
| … | 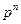
|
Сумма вероятностей 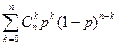 =
= 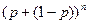 =1.
=1.
Определение 13.5. Говорят, что дискретная форма случайной величины Х имеет распределение Пуассона с параметром 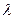 (
(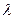 > 0), если она принимает целые значения k
> 0), если она принимает целые значения k 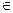 {0, 1, 2, …} с вероятностями Р(Х=k)=
{0, 1, 2, …} с вероятностями Р(Х=k)= 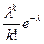 .
.
Ряд распределения имеет вид
| Х | … | k | … | ||
| Р | 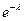
| 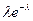
| … | 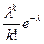
| … |
Так как разложение 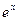 в ряд Маклорена имеет следующий вид
в ряд Маклорена имеет следующий вид 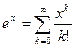 , тогда сумма вероятностей
, тогда сумма вероятностей 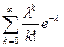 =
= 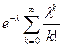 =
= 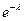
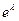 =1.
=1.
Обозначим через Х число испытаний, которые нужно провести до первого появления события А в независимых испытаниях, если вероятность появления А в каждом из них равна p (0< p < 1), а вероятность непоявления 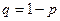 . Возможными значениями Х являются натуральные числа.
. Возможными значениями Х являются натуральные числа.
Определение 13.6. Говорят, что случайная величина Х имеет геометрическое распределение с параметром p (0< p < 1), если она принимает натуральные значения k 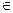 N с вероятностями Р(Х=k)=
N с вероятностями Р(Х=k)= 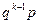 , где
, где 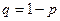 . Ряд распределения:
. Ряд распределения:
| Х | … | n | … | |||
| Р | 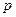
| 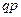
| 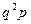
| … | 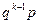
| … |
Сумма вероятностей 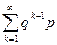 =
= 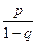 =
= 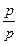 =1.
=1.
Пример 13.7. Монета брошена 2 раза. Составить ряд распределения случайной величины Х  числа выпадений «герба».
числа выпадений «герба».
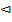 P2(0)=
P2(0)= 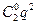 =
= 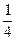 ; P2(1)=
; P2(1)= 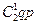 =
=  =0, 5; P2(2)=
=0, 5; P2(2)= 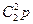 =
= 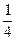 .
.
| Х | |||
| Р | 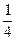
| 
| 
|
Ряд распределения примет вид:
. 
Пример 13.8. Из орудия стреляют до первого попадания по цели. Вероятность попадания при одном выстреле 0, 6. 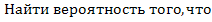 произойдёт попадание при 3-м выстреле.
произойдёт попадание при 3-м выстреле.
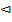 Поскольку p =0, 6, q =0, 4, k =3, тогда Р(А)=
Поскольку p =0, 6, q =0, 4, k =3, тогда Р(А)= 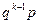 =0, 42*0, 6=0, 096.
=0, 42*0, 6=0, 096. 
14 Числовые характеристики дискретных случайных величин
Полностью характеризует случайную величину закон распределения, однако часто он бывает неизвестен, поэтому приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами (параметрами), описывающими случайную величину суммарно. Они называются числовыми характеристиками случайной величины. К ним относятся: математическое ожидание, дисперсия и др.
Определение 14.1. Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через М Х =М(Х)=Е Х.
Если случайная величина Х принимает конечное число значений, то М Х = 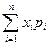 .
.
Если случайная величина Х принимает счетное число значений, то М Х = 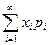 ,
,
причём математическое ожидание существует, если ряд сходится абсолютно.
Замечание 14.2. Математическое ожидание  некоторое число, приближённо равное определённому значению случайной величины.
некоторое число, приближённо равное определённому значению случайной величины.
Пример 14.3. Найти математическое ожидание случайной величины Х, зная её ряд распределения
| Х | |||
| Р | 0, 1 | 0, 6 | 0, 3 |
 М Х =3*0, 1+5*0, 6+2*0, 3=3, 9.
М Х =3*0, 1+5*0, 6+2*0, 3=3, 9. 
Пример 14.4. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна p.
 Случайная величина Х – число появления события A в одном испытании. Она может принимать значения
Случайная величина Х – число появления события A в одном испытании. Она может принимать значения 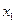 =1 (A наступило) с вероятностью p и
=1 (A наступило) с вероятностью p и 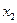 =0 с вероятностью
=0 с вероятностью 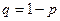 , т.е. ряд распределения
, т.е. ряд распределения
| Х | ||
| Р | p | q |
М Х = 1∙ p +0∙ q = p. 
Т.е., математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Свойства математического ожидания
Свойство 14.5. Математическое ожидание постоянной величины равно самой постоянной: МС=С.
 Будем рассматривать постоянную С как дискретную случайную величину с рядом
Будем рассматривать постоянную С как дискретную случайную величину с рядом
| С | C |
| Р |
Отсюда МС=С*1=С. 
Замечание 14.6. Произведение постоянной величины С на дискретную случайную величину Х Определяется как дискретная случайная величина С Х, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности этих значений С Х равны вероятностям соответствующих возможных значений Х.
Свойство 14.7. Постоянный множитель можно выносить за знак математического ожидания:
М(С Х)=С∙ М Х.
 Если случайная величина Х имеет ряд распределения
Если случайная величина Х имеет ряд распределения
| Х | 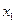
| 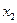
| … | 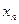
| … |
| Р | 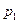
| 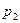
| … | 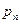
| … |
Ряд распределения случайной величины
| СХ | 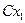
| 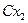
| … | 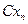
| … |
| Р | 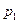
| 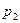
| … | 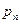
| … |
М(С Х)= 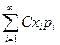 =
= 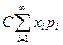 = С∙ М(Х).
= С∙ М(Х). 
Определение 14.8. Случайные величины 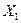 ,
, 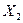 , …,
, …, 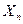 называются независимыми, если для
называются независимыми, если для 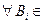
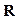 , i =1, 2, …, n
, i =1, 2, …, n
Р{ 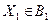 ,
, 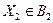 , …,
, …, 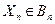 }= Р{
}= Р{ 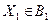 } Р{
} Р{ 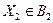 }… Р{
}… Р{ 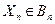 } (1)
} (1)
Если в качестве 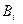 =
= 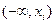 , i =1, 2, …, n, то получим из (1)
, i =1, 2, …, n, то получим из (1)
Р{ 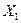 <
< 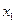 ,
, 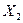 <
< 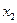 , …,
, …, 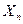 <
< 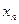 }= Р{
}= Р{ 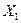 <
< 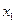 }Р{
}Р{ 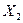 <
< 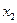 }… Р{
}… Р{ 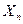 <
< 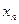 }, откуда получается другая формула:
}, откуда получается другая формула:
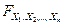 (
(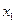 ,
, 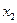 , …,
, …, 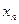 ) =
) = 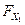 (
(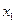 )
) 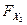 (
(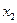 )...
)... 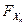 (
(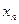 ) (2)
) (2)
для совместной функции распределения случайных величин 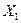 ,
, 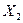 , …,
, …, 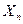 , которую можно также взять в качестве определения независимости случайной величины.
, которую можно также взять в качестве определения независимости случайной величины.
Свойство 14.9. Математическое ожидание произведения 2-х независимых случайных величин равно произведению их математических ожиданий:
М(ХУ)=М Х ∙ М У.
Свойство 14.10. Математическое ожидание суммы 2-х случайных величин равно сумме их математических ожиданий:
М(Х+У)=М Х +М У.
Замечание 14.11. Свойства 14.9 и 14.10 можно обобщать на случай нескольких случайных величин.
Пример 14.12. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании 2-х игровых костей.
 Пусть Х
Пусть Х  число очков, выпавших на первой кости, У
число очков, выпавших на первой кости, У  число очков, выпавших на второй кости. Они имеют одинаковые ряды распределения:
число очков, выпавших на второй кости. Они имеют одинаковые ряды распределения:
| Х | ||||||
| Р | 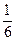
| 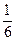
| 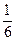
| 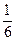
| 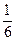
| 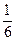
|
Тогда М Х =М У = 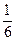 (1+2+3+4+5+6)=
(1+2+3+4+5+6)= 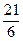 =
=  . М(Х+У)=2*
. М(Х+У)=2*  =7.
=7. 
Теорема 14.13. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: М Х = np.
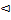 Пусть Х – число появлений события А в n независимых испытаниях.
Пусть Х – число появлений события А в n независимых испытаниях. 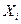 –число появлений события А в i -том испытании, i =1, 2, …, n. Тогда
–число появлений события А в i -том испытании, i =1, 2, …, n. Тогда 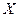 =
= 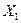 +
+ 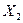 +…+
+…+ 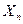 . По свойствам математического ожидания М Х =
. По свойствам математического ожидания М Х = 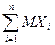 . Из примера 14.4 M Xi = p, i =1, 2, …, n, отсюда М Х =
. Из примера 14.4 M Xi = p, i =1, 2, …, n, отсюда М Х = 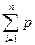 = np.
= np. 
Определение 14.14. Дисперсией случайной величины называется число D X =M(X -M X)2.
Определение 14.15. Средним квадратическим отклонением случайной величины Х называется число 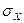 =
= 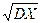 .
.
Замечание 14.16. Дисперсия является мерой разброса значений случайной величины вокруг её математического ожидания. Она всегда неотрицательна. Для подсчёта дисперсии удобнее пользоваться другой формулой:
D X = M(X - M X)2 = M(X 2 - 2 X∙ M X + (M X)2) = M(X 2) - 2M(X∙ M X) + M(M X)2= =M(X 2)-M X∙ M X+ (M X)2 = M(X 2) - (M X)2.
Отсюда D X = M(X 2) - (M X)2.
Пример 14.17. Найти дисперсию случайной величины Х, Заданной рядом распределения
| X | |||
| P | 0, 1 | 0, 6 | 0, 3 |
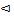 M X =2*0, 1+3*0, 6+5*0, 3=3, 5; M(X 2)= 4*0, 1+9*0, 6+25*0, 3=13, 3;
M X =2*0, 1+3*0, 6+5*0, 3=3, 5; M(X 2)= 4*0, 1+9*0, 6+25*0, 3=13, 3;
D X =13.3-(3, 5)2=1, 05. 
Свойства дисперсии
Свойство 14.18. Дисперсия постоянной величины равна 0:
DC=0
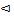 DC = M(С- MС)2= M(С- С)2=0.
DC = M(С- MС)2= M(С- С)2=0. 
Свойство 14.19. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
D(С X) =C2 D X.
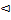 D(CХ)=М(С- CM X)2=М(С(X- M X)2) = C2 M(X - M X)2 = C2D X.
D(CХ)=М(С- CM X)2=М(С(X- M X)2) = C2 M(X - M X)2 = C2D X. 
Свойство 14.20. Дисперсия суммы 2-х независимых случайных величин равна сумме дисперсий этих величин
D(Х+Y)=D Х +D Y.
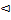 D(X + У)=М((X + Y)2) – (M(X + Y))2= M(X2 + 2 XY + Y2) - (M X + M Y)2= =M(X)2+2М Х М Y +M(Y 2)-(M(X)2+2М Х М Y +M(Y)2)= M(X 2)-(M X)2+M(Y 2)- (M Y)2= = D X +D Y.
D(X + У)=М((X + Y)2) – (M(X + Y))2= M(X2 + 2 XY + Y2) - (M X + M Y)2= =M(X)2+2М Х М Y +M(Y 2)-(M(X)2+2М Х М Y +M(Y)2)= M(X 2)-(M X)2+M(Y 2)- (M Y)2= = D X +D Y. 
Следствие 14.21. Дисперсия суммы нескольких независимых случайных величин равна сумме их дисперсий.
Теорема 14.22. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в данном испытании.
D X = npq.
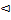 X – число появлений события А в n независимых испытаниях, Х =
X – число появлений события А в n независимых испытаниях, Х = 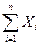 , где
, где 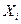 – число появлений A в i -том испытании, взаимно независимые, поскольку исход каждого испытания не зависит от исходов остальных.
– число появлений A в i -том испытании, взаимно независимые, поскольку исход каждого испытания не зависит от исходов остальных.
D X = 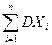 ,
,
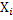
| ||
| Р | p | q |
Получаем, что М 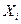 = p и M
= p и M 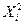 = p, тогда D
= p, тогда D 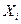 =M(
=M(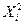 )-(М
)-(М 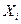 )2= p-p2 = p (1 -p)= pq. Следовательно D X =
)2= p-p2 = p (1 -p)= pq. Следовательно D X = 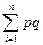 = npq.
= npq. 
Пример 14.23. Проводятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0, 6. Найти дисперсию Х - числа появлений события в этих испытаниях.
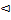 Поскольку n =10, p =0, 6, q =0, 4, тогда D X = npq =10*0, 6*0, 4=2, 4.
Поскольку n =10, p =0, 6, q =0, 4, тогда D X = npq =10*0, 6*0, 4=2, 4. 
Определение 14.24. Начальным моментом порядка k случайной величины Х называют математическое ожидание случайной величины  :
:
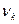 =M(
=M( ).
).
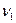 =M(
=M(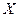 ),
), 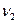 =M(
=M(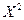 ). Отсюда D X =
). Отсюда D X = 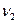 -
- 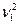 .
.
Определение 14.25. Центральным моментом порядка k случайной величины Х называется математическое ожидание случайной величины (X -M X)k.
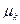 =М[(X -M X)k].
=М[(X -M X)k].
Таким образом, 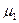 = М[ X -M X ]= M X - M X =0,
= М[ X -M X ]= M X - M X =0, 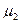 = М[(X -M X)2]= D X. Следовательно
= М[(X -M X)2]= D X. Следовательно 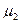 =
= 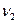 -
- 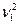 .
.
По определению центрального момента и пользуясь свойствами математического ожидания можно получить формулы для моментов более высоких порядков:
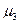 =
= 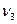 -3
-3 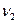
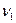 +2
+2 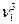 ,
,
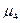 =
= 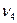 -4
-4 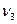
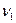 +6
+6 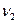
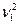 -3
-3 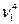 .
.