
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формулы полной вероятности и Байеса
|
|
Теорема 9.1. (формула полной вероятности) Если события H1, H2, …, Hn образуют полную группу, то вероятность появления события А, которое может произойти совместно с любым из событий Hi, i 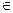 {1, …, n }, находится по формуле:
{1, …, n }, находится по формуле:
Р(А)=Р(H1)P(A | H1) + … + Р(Hn)P(A | Hn) или Р(А)= 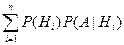 .
.
 Поскольку события образуют полную группу, то Ω = H1+H2+…+Hn. Событие А происходит только с одним из событий Hi, i
Поскольку события образуют полную группу, то Ω = H1+H2+…+Hn. Событие А происходит только с одним из событий Hi, i 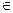 {1, …, n }, поэтому A ∙ Ω = А = А∙ H1+ А∙ H2+…+ А∙ Hn. По теореме сложения вероятностей Р(А)=Р(А∙ H1)+…+Р(А∙ Hn)=Р(H1)Р(А|H1)+…+Р(Hn)Р(А | H1)
{1, …, n }, поэтому A ∙ Ω = А = А∙ H1+ А∙ H2+…+ А∙ Hn. По теореме сложения вероятностей Р(А)=Р(А∙ H1)+…+Р(А∙ Hn)=Р(H1)Р(А|H1)+…+Р(Hn)Р(А | H1) 
Пример 9.2. Имеются две урны. В первой – 3 белых и 5 чёрных шаров, во второй – 4 белых и 3 чёрных. Из 1-й урны наудачу взят 1 шар и переложен во 2-ю урну. После этого из 2-й урны извлечён наудачу шар. Какова вероятность того, что он белый?
 А – из 2-й урны извлечён белый шар,
А – из 2-й урны извлечён белый шар,
H1 – из 1-й урны во 2-ю переложен белый шар,
H2 – из 1-й урны во 2-ю переложен чёрный шар, H1 + H2 =Ω.
Р(А)=Р(H1)Р(А | H1)+Р(H2)Р(А| H2)= 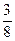 ∙
∙ 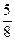 +
+ 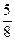 ∙
∙ 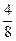 =
= 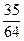
Замечание 9.3. При применении формулы полной вероятности события H1, H2, …, Hn, образующие полную группу, называются гипотезами.
Теорема 9.4. (формула Байеса) Пусть события H1, H2, …, Hn образуют полную группу, А – некоторое событие, которое может произойти совместно с любым из событий Hi, i 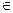 {1, …, n }, тогда условная вероятность:
{1, …, n }, тогда условная вероятность:
Р(Hj | А) = 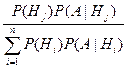 , j
, j 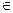 {1, 2, …, n }.
{1, 2, …, n }.
 Р(Hj | А) =
Р(Hj | А) = 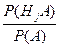 =
= 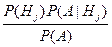 =
= 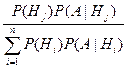 .
. 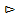
Пример 9.5. Рассмотрим предыдущий пример с учётом того, что из 2-й урны вынули белый шар. Найти вероятность того, что из 1-й урны во 2-ю переложили белый шар.
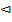 Р(H1 | А) =
Р(H1 | А) = 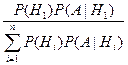 =
= 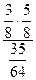 =
= 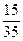 =
= 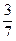 .
. 
Замечание 9.6. В формуле Байеса вероятности Р(Hi), i 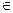 {1, …, n } называются априорными вероятностями гипотез. Вероятности Р(Hi|A), i
{1, …, n } называются априорными вероятностями гипотез. Вероятности Р(Hi|A), i 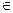 {1, …, n } называются апостериорными вероятностями гипотез.
{1, …, n } называются апостериорными вероятностями гипотез.