
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аксиомы теории вероятностей. Дискретные пространства элементарных исходов. Классическое определение вероятности
|
|
Пусть Ω пространство элементарных исходов, F – множество всех подмножеств Ω. Любому событию A 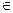 F ставится в соответствие действительное число P(A), называемое вероятностью события A, при этом выполняются аксиомы теории вероятности:
F ставится в соответствие действительное число P(A), называемое вероятностью события A, при этом выполняются аксиомы теории вероятности:
Аксиома 4.1. Вероятность произвольного события неотрицательна, т.е. 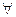 A
A 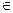 F, P(A)
F, P(A) 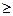 0.
0.
Аксиома 4.2. Вероятность достоверного события равна 1, т.е. P(Ω)=1.
Аксиома 4.3. (счетной аддитивности) Если A1, A2, … 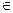 F и Ai∙ Aj= Ø (i
F и Ai∙ Aj= Ø (i 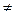 j), то P(A1+ A2+…) = P(A1) + P(A2) +… или P(
j), то P(A1+ A2+…) = P(A1) + P(A2) +… или P( ) =
) = 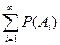 .
.
Определение 4.4. Бесконечное множество называется счетным, если элементы этого множества можно занумеровать натуральными числами.
Все другие множества называются несчетными (например, множество точек [a, b] ненулевой длины).
Определение 4.5. Пространство элементарных исходов называется дискретным, если оно конечное или счетное, т.е. Ω ={ω 1, …, ω n} или Ω ={ω 1, ω 2, … }.
Любому элементарному исходу ω i ставится в соответствие число p(ω i), так что при этом 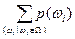 =1.
=1.
Определение 4.6. Вероятностью события A называется число P(A)= 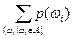 .
.
Пример 4.7. Бросается игральная кость. Найти вероятность выпадения нечетного числа очков.
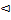 p(ω i)=
p(ω i)= 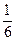 , i =1,.., 6,
, i =1,.., 6,  P(A)= p(ω 1, ω 3, ω 5)=
P(A)= p(ω 1, ω 3, ω 5)= 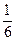 +
+ 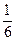 +
+ 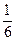 =
= 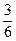 =
=  .
. 
Сформулируем следующие предположения:
1. Пространство элементарных исходов конечно: Ω ={ω 1, …, ω n}.
2. Все элементарные исходы равновероятны (равновозможны), т.е. p(ω 1)= p(ω 2)=…= p(ω n).
Поскольку 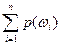 =1, то p(ω i)=
=1, то p(ω i)= 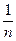 , i =1,.., n.
, i =1,.., n.
Рассмотрим некоторое событие A 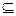 Ω, состоящее из k элементарных исходов, k
Ω, состоящее из k элементарных исходов, k 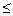 n, A= {
n, A= { 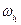 ,
, 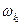 , …,
, …, 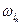 }.
}.
Вероятность события P(A)= 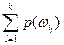 =
= 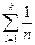 =
=  .
.
Определение 4.8. (классическое определение вероятности) Если пространство элементарных исходов конечно, а все элементарные исходы равновероятны, то вероятность события A называется отношение числа элементарных исходов, благоприятствующих A, к общему числу всех возможных элементарных исходов P(A)=  .
.
Пример 4.9. Бросается две монеты. Найти вероятность того, что хотя бы на одной выпадет герб.
 Ω ={(г, г), (г, р), (р, г), (р, р)}, n= 4.
Ω ={(г, г), (г, р), (р, г), (р, р)}, n= 4.
A= {(г, г), (г, р), (р, г)}, k =3.
Таким образом, P(A)=  =
= 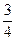 .
. 
Пример 4.10. Бросаются две игральные кости. Какова вероятность того, что сумма выпавших очков равна 7?
 Ω ={(i, j) | i, j
Ω ={(i, j) | i, j 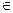 {1,.., 6}}, n= 36,
{1,.., 6}}, n= 36,
A= { (6, 1), (5, 2), (4, 3), (3, 5), (2, 5), (1, 6)}, k =6,
Таким образом, P(A)=  =
=  =
= 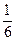 .
. 