
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предмет и задачи теории вероятностей. События и операции над ними. Относительные частоты и их свойства
|
|
Возникновение теории вероятностей относят к XVII веку и связывают с решением комбинаторных задач теории азартных игр и потребностями страхового дела. Азартные игры (карты, кости) дали стимул для построения математических моделей игровых ситуаций. Эти модели предоставляли игроку возможность ориентироваться в ходе игры, делать расчеты ставок, оценивать шансы выигрыша, а также позволяли планировать расходы и доходы страховых компаний и т.д.
Разработкой таких моделей занимались в 17 веке Б. Паскаль, П. Ферма, Х. Гюйгенс. Основы классической теории вероятности были сформулированы в 18 веке Я. Бернулли, П. Лапласом, С. Пуассоном, К. Гауссом. В 1933году А.Н. Колмогоров сформулировал аксиомы теории вероятности, базирующиеся на теории множеств.
Однако с теорией вероятностей развивалась и другая современная дисциплина – математическая статистика, которая широко применяется в экономике, технике, социологии, медицине, физике, лингвистическом программировании и др.
Определение 3.1. Предметом теории вероятностей является количественный и качественный анализ математических моделей вероятностных экспериментов, называемый статистической обработкой экспериментальных данных.
Вероятностные эксперименты имеют следующие общие черты: непредвиденность результата; наличие определенных количественных закономерностей при их многократном повторении при одинаковых условиях; множество возможных исходов.
Определение 3.2. Вероятностными называют эксперименты, которые можно повторить произвольное число раз при соблюдении одних и тех же стабильных условий, однако их исходы неоднозначны, случайны.
Определение 3.3. Теория вероятностей – наука, занимающаяся анализом математических моделей для принятия решений в условиях неопределенности.
Первичным понятием теории вероятности, не определенным через другие понятия, является пространство элементарных исходов Ω.
Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента.
Пример 3.4. Приведем примерыпространств элементарных исходов:
1) При бросании симметричной монеты в качестве Ω выбирается Ω ={г, р}.
2) При бросании игральной кости пространство элементарных исходов следующее Ω ={1, 2, 3, 4, 5, 6}.
3) При бросании двух симметричных монет Ω ={(р, р), (р, г), (г, р), (г, г)}.
 4) При бросании двух игральных костей Ω ={(i, j) | i, j
4) При бросании двух игральных костей Ω ={(i, j) | i, j 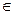 {1, …, 6}}, n=36.
{1, …, 6}}, n=36.
 5) Пусть на [AB] наудачу бросается точка Ω ={ω | ω
5) Пусть на [AB] наудачу бросается точка Ω ={ω | ω 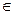 [AB]}=[AB].
[AB]}=[AB].
6) Пусть на [AB] наудачу бросаются две точки
Ω ={(x, y) | x 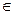 [AB], y
[AB], y 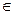 [AB]}=[AB]× [AB].
[AB]}=[AB]× [AB].
Определение 3.5. Опытом или испытанием называют всякое осуществление определённого комплекса условий или действий, при которых происходит соответствующее явление. Возможный результат опыта называют событием, те событием называется произвольное подмножество A пространства элементарных исходов Ω.
Пример 3.6. Опытом является подбрасывание монеты, а событиями “герб”, “цифра на верхней ее стороне” (когда монета упадет). Опытами являются стрельба по мишени, извлечение шара из ящика и т.п. События будем обозначать заглавными буквами латинского алфавита А, В, С.
Определение 3.7. Каждое событие, которое может наступить в итоге опыта, называется элементарным исходом (элементарным событием, или шансом).
Определение 3.8. Элементарные исходы, при которых данное событие наступает, называются благоприятствующими этому событию, или благоприятными шансами, т.е. те элементарные исходы, из которых состоит событие A, называются благоприятствующими событию A.
Пример 3.9. Так, при подбрасывании игрального кубика элементарные исходы А1, А3, А5 являются благоприятствующими событию “выпало нечетно число очков”.
Говорят, что событие A произошло, если в результате эксперимента происходит элементарный исход благоприятствующий событию A, т.е. ω 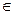 A.
A.
Определение 3.10. Событие называется достоверным, в данном опыте, если оно обязательно произойдет в этом опыте, т.е. все пространство элементарных исходов Ω, если его взять в качестве события, называют достоверным событием, поскольку оно происходит в любом эксперименте (всегда).
Пример 3.11. Если в ящике только голубые шары, то событие “из ящика извлечен голубой шар” является достоверным (в ящике нет шаров другого цвета).
Определение 3.12. Событие называется невозможным, в данном опыте, если оно не может произойти в этом опыте.
Пустое множество Ø (т.е. множество, не содержащее ни одного элементарного исхода) называется невозможным событием, поскольку оно никогда не произойдет.
Пример 3.13. Так, если в ящике находятся только красные шары, то событие “из ящика извечен голубой шар” является невозможным (таких шаров в ящике нет).
Определение 3.14. Событие называется случайным в данном опыте, если око может произойти, а может и не произойти в этом опыте, т.е. все остальные события, кроме достоверного и невозможного, называются случайными.
Пример 3.15. Если в ящике находятся n голубых и m красных шаров, одинаковы по размеру и весу, то событие “из урны извлечен голубой шар” является случайным (оно может произойти, а может и не произойти, поскольку в урне имеются не только голубые, но и красные шары). Случайными событиями являются “герб” и “цифра на верхней стороне монеты при ее подбрасывании”, “попадание и промах при стрельбе по мишени”, “выигрыш по билету лотереи” и т.п.
Замечание 3.16. Приведенные примеры свидетельствуют о том, что одно и то же событие в некотором опыте может быть достоверным, в другом – невозможным, в третьем - случайным. Говоря о достоверности, невозможности, случайности события, имеют в виду его достоверность, невозможность, случайность по отношению к конкретному опыту, т.е. к наличию определенного комплекса условий или действий.
Определение 3.17. Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого в этом опыте.
Пример 3.18. Так, при подбрасывании двух симметричных монет, событие A – «герб на верхней стороне первой монеты” и B – “цифра на верхней стороне второй монеты” являются совместными.
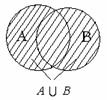 Операции над событиями.
Операции над событиями.
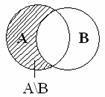
Определение 3.19. Суммой событий A и B называют объединение этих множеств A 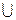 B.
B.
Обозначают A + B= { x | x 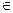 A или x
A или x 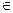 B }.
B }.
Вместо союза или – ставится знак 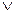 .
.
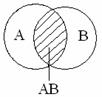 Определение 3.20. Произведением событий A и B называют пересечение множеств A
Определение 3.20. Произведением событий A и B называют пересечение множеств A 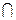 B.
B.
Обозначают AB= { x | x 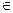 A и x
A и x 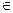 B }.
B }.
 Вместо союза и – ставятся знаки
Вместо союза и – ставятся знаки 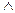 , &.
, &.
Определение 3.21. Разностью событий A и B называют разность множеств A \ B.
Обозначают A \ B= { x | x 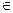 A и x
A и x 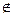 B }.
B }.
 Определение 3.22. Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании, т.е. события A и B называются несовместимыми (несовместными), если AB = Ø.
Определение 3.22. Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании, т.е. события A и B называются несовместимыми (несовместными), если AB = Ø.
Если AB = Ø, то будем говорить, что A 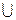 B= A + B.
B= A + B.
Так, несовместными являются попадание и промах при одном выстреле.
 Несколько событий называются несовместными, если они попарно несовместны.
Несколько событий называются несовместными, если они попарно несовместны.
Определение 3.23. Говорят, что событие A влечет событие B, если A 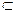 B.
B.
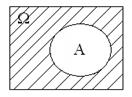 Определение 3.24. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из противоположных событий обозначено буквой A, то другое обозначают Ā. Таким образом событие Ā = Ω \ A называется противоположным к событию A.
Определение 3.24. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из противоположных событий обозначено буквой A, то другое обозначают Ā. Таким образом событие Ā = Ω \ A называется противоположным к событию A.
Пример 3.25. 1)Так, противоположными являются события “герб” и “цифра” при одном подбрасывании симметричной монеты.
2) Если A – “попадание”, то Ā – “промах” при одном выстреле по мишени.
3) При бросании игральной кости Ω ={1, 2, 3, 4, 5, 6}. Если A – выпадение нечетного числа очков, т.е. A ={1, 3, 5, }, то Ā ={2, 4, 6} – противоположное событие (выпадение четного числа очков).
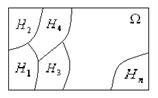 Определение 3.26. Множество событий H1, H2, …, Hn называют полной группой событий, если они попарно-несовместны; появление одного и только одного из них является достоверным событием.
Определение 3.26. Множество событий H1, H2, …, Hn называют полной группой событий, если они попарно-несовместны; появление одного и только одного из них является достоверным событием.
Таким образом события H1, H2, …, Hn образуют полную группу, если H1+ H2+…+ Hn= Ω (т.е. Hi Hj= Ø, если i 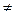 j).
j).
В частности события A и Ā образуют полную группу, т.к. A + Ā = Ω.
Пример 3.27. Рассмотрим события, появляющиеся при подбрасывании игрального кубика (т.е. кубика, на гранях которого записаны цифры 1, 2, 3, 4, 5, 6 или изображены знаки, соответствующие этим цифрам). Когда кубик упадет, то верхней гранью окажется грань с одной из этих цифр. Событие: “верхней гранью оказалась грань с цифрой k ” обозначим через Аk (k =1, 2, 3, 4, 5, 6). События А1, А2, А3, А4, А5, А6 образуют полную группу: они попарно-несовместны; появление одного и только одного из них является достоверным событием (когда кубик упадет, то только одна из граней окажется верхней, на ней написана только одна цифра от 1 до 6).
Определение 3.28. События считают равновозможными, если нет оснований полагать, что одно событие является более возможным, чем другие.
Пример 3.29. При подбрасывании монеты событие A (появление цифры) и событие B (появление герба) равновозможны, так как предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не влияет на то, какая сторона монеты (герб или цифра) окажется верхней. При подбрасывании игрального кубика события А1, А2, А3, А4, А5, А6 являются равновозможными, поскольку предполагается, что кубик изготовлен из однородного материала, имеет правильную форму и наличие цифр (или очков) на гранях не влияет на то, какая из шести граней окажется верхней.
Относительные частоты и их свойства.
Пусть производится некоторый случайный (вероятностный) эксперимент, пространством элементарных исходов является множество Ω. Рассмотрим некоторое событие A (A 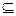 Ω). Если эксперимент произвести N раз, а событие A появится в них N(A) раз, то число W(A)=
Ω). Если эксперимент произвести N раз, а событие A появится в них N(A) раз, то число W(A)= 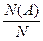 называется относительной частотой появления события A.
называется относительной частотой появления события A.
Свойство 3.30. Относительная частота произвольного события неотрицательна, т.е. 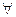 A
A 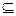 Ω, W(A)
Ω, W(A) 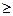 0.
0.
Свойство 3.31. Относительная частота достоверного события равна 1.
W(A)= 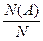 =
= 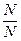 =1.
=1.
Свойство 3.32. (аддитивности). Относительная частота суммы несовместных событий равна сумме относительных частот этих событий.
W(A+B)= 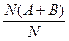 =
= 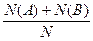 =
= 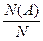 +
+ 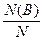 = W(A)+ W(B).
= W(A)+ W(B).