Распределение Пуассона.

Рассматривается схема Бернулли. Число независимых испытаний п велико, а вероятность события мала (р< =0.1).

В этом случае формула Лапласа непригодна. Поэтому прибегают к асимптотической формуле Пуассона.

Т.о. перед нами задача: найти вероятность того, что при очень большом числе испытании, в каждом из которых вероятность события очень мала, событие наступит ровно k раз.

Сделаем важное предположение: произведение n*p сохраняет постоянное значение (np=λ). Это означает, что среднее число появления события в различных сериях испытаний (т.е. при различных значениях п) остается неизменным:

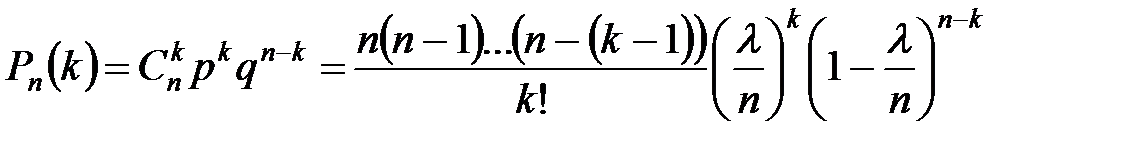
Т.к. п очень велико, вместо Р_n(k) найдем 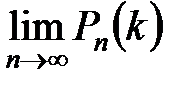и его будем считать приближенным значением вероятности Р_n(k):

.

.

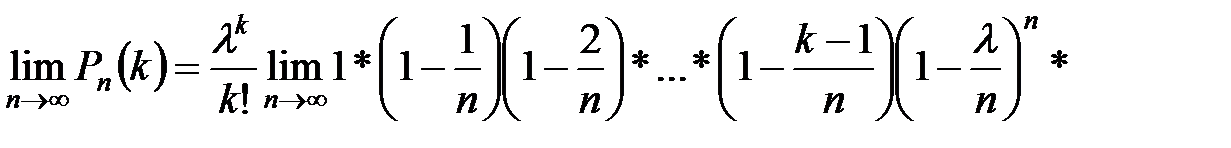
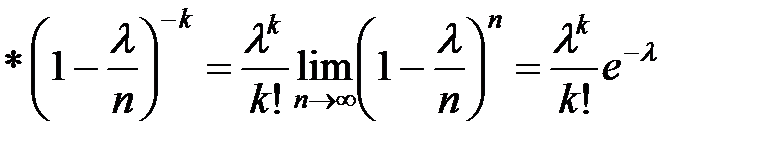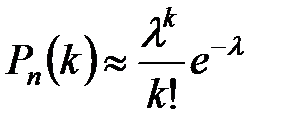Рассмотрим СВ Х, которая принимает значения 0, 1, 2, …

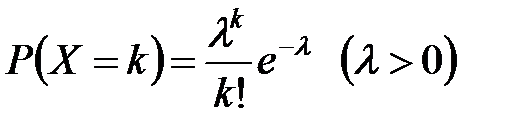
В этом случае говорят, что СВ Х имеет закон распределения Пуассона.

Закон распределения Пуассона можно задать в виде таблицы:

Х	0	1	2	…	k	…
p	e-λ	λ e-λ		…		…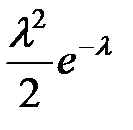

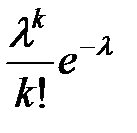
Заметим, что