Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывные СВ.
|
|
Опр. СВ Х наз-ся непрерывной СВ, если существует такая неотрицательная, интегрируемая по Риману на (-∞, +∞) ф-ция р(х) (f(x)), что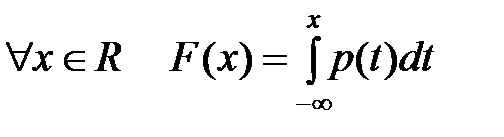 
.
Ф-ция р(х) называется плотностью распределения вероятности СВ Х.
Плотность p(x) обладает след. свойствами:
1) 
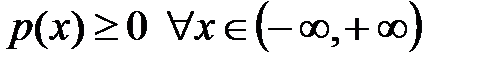
2) 
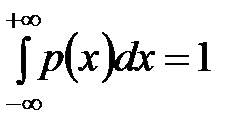- условие нормирования
3) F`(x)=p(x) в точках непрерывности функции p(x).
Вывод: Ф-ция распределения непрерывной СВ является непрерывной, монотонно-неубывающей ф-цией на все числовой оси.
P(X=x)=F(x+0)-F(x) (следует из того, что P(x< =X< x+Δ х)= =F(x+Δ х)-F(x)). Если Х – непрерывная СВ, то F(x+0)-F(x)=0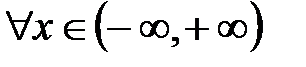 
. Т.о. для непрерывной СВ Р(Х=х)=0. Говорят, что вероятность попасть в точку равна 0.
Если Х – непрерывная СВ, то вероятность ее попадания на [a, b) можно вычислить через плотность распределения вероятностей по формуле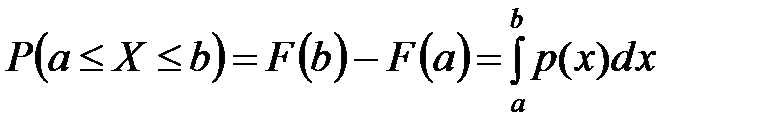 
.
Если х – точка непр. плотности вероятности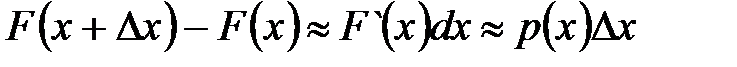 
. Формула справедлива с точностью до бесконечно малых величин высшего порядка малости, чем Δ х.