Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства функции распределения.
|
|
1) 
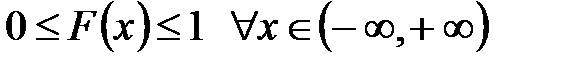, т.к. F(x) – вероятность.
2) F(x) не убывает на все числовой оси.
Док-во: Возьмем х1< x2. Рассмотрим вероятность того, что Х< x2: P(X< x2). A={X< x2}. B={x1< =X< x2}. A+B={X< x2}. События А и В несовместны. Значит, P(A+B)=P(A)+P(B)= =F(x2)=F(x1)+P(x1< =X< x2). Последнее слагаемое в равенстве > =0. Значит, F(x2)> = F(x1). Доказано.
3) P(x1< =X< x2)=F(x2)-F(x1)
4) Функция распределения F(x) всегда непрерывна.
Док-во: Аксиома 3 из определения вероятности (если А1, А2, …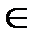 
F (F- алгебра ), причем Ai*Aj =Ø для i 
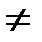j, то Р(А1+А2+…) = 
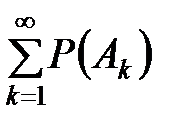) эквивалентна аксиоме непрерывности (если В1, В2, …, Вk, … - последоват. таких событий, что Bn+1 
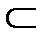Bn, n=1, 2, … и 
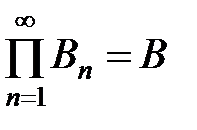, то 
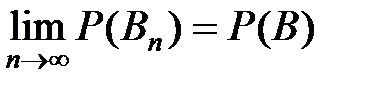). Доказать самостоятельно эквивалентность аксиом. Непрерывность функции F(x) будем док-ть с помощью определения предела по Гейне: х1, х2, …, хn – любая последовательность, удовлетворяющая двум условиям:
1) х1< х2< …< хn< …< x0;
2) 
.
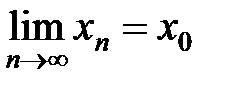Событие An={xn< =X< x0}, An+1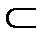 
An. Согласно аксиоме непрерывности:
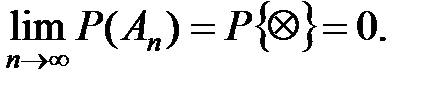
Р(Аn)=P(xn< =X< x0)=F(x0)-F(xn).
.
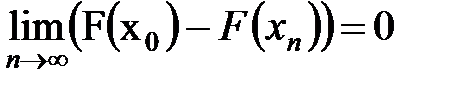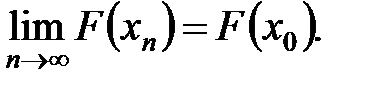
По Гейне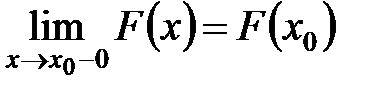 
. Значит, функция непрерывна слева. Доказано.
5) 
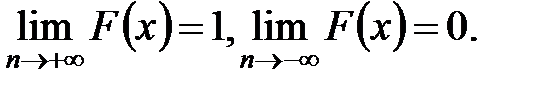
Док-во: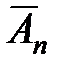 
={X< п}, An={X> =n}, An+1 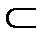An.
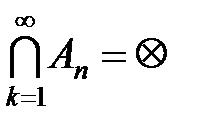
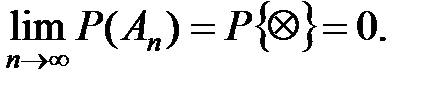
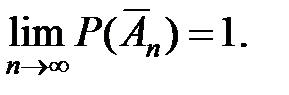
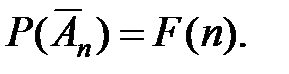
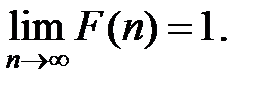Доказано.