
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Правило Крамера
|
|
Правило Крамера рассмотрим на примере двух линейных уравнений с двумя переменными:
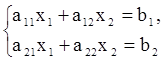 (1)
(1)
хотя оно применимо и для решения системы n линейных уравнений с n переменными, но с увеличением n требует большого объема вычислительной работы.
Умножим первое уравнение системы (1) на коэффициент а22, а второе — на — a12 и полученные уравнения сложим. Тогда имеем:
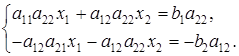
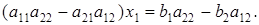
Если a11a22 - a21a12 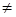 0, то получаем значение переменной
0, то получаем значение переменной 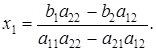
Аналогично, умножая первое уравнение системы (1) на —a21, второе — на а11 и складывая их, получаем:
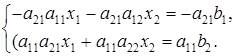
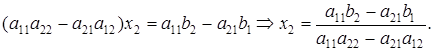
Введем обозначения: a11a22 - a21a12 = 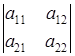 =
= 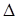 ;
;
b1a22 - b2a12 = 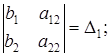
a11b2 - a21b1 = 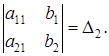
Следовательно, 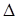 — определитель матрицы коэффициентов системы (1). Определитель
— определитель матрицы коэффициентов системы (1). Определитель 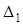 получается из определителя
получается из определителя 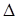 , если коэффициенты системы (1) при x1 (первый столбец матрицы А ) заменить свободными членами B =
, если коэффициенты системы (1) при x1 (первый столбец матрицы А ) заменить свободными членами B = 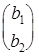 ;
;
Определитель 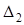 — если заменить коэффициенты системы (1) при x2 (второй столбец матрицы А ) свободными членами.
— если заменить коэффициенты системы (1) при x2 (второй столбец матрицы А ) свободными членами.
Определитель 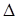 называется главным определителем системы (1), а определители
называется главным определителем системы (1), а определители 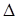 1 и
1 и 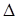 2 — вспомогательными.
2 — вспомогательными.
Если главный определитель 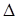
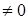 , то матрица
, то матрица 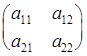 называется неособенной, в противном случае - особенной.
называется неособенной, в противном случае - особенной.
Таким образом, если главный определитель системы уравнений (1) 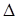
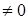 , то система имеет единственное решение, определяемое формулами
, то система имеет единственное решение, определяемое формулами
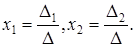 (2)
(2)
Формулы (2) называются формулами Крамера.
Нахождение решения линейной системы (1) по формулам (2) называется правилом Крамера, который одним из первых пришел к понятию определителя и доказал сформулированное выше предложение.
Справедливы также следующие два предложения:
1. Если главный определитель системы (1) 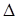 = 0, но хотя бы один из вспомогательных определителей
= 0, но хотя бы один из вспомогательных определителей 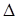 1 или
1 или 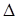 2 отличен от нуля, то система (1) не имеет решений (система несовместна).
2 отличен от нуля, то система (1) не имеет решений (система несовместна).
2. Если все три определителя 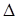 ,
, 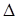 1 и
1 и 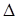 2 системы (1) равны нулю, но среди коэффициентов аij(i, j = 1, 2) есть хотя бы один, отличный от нуля, то система (1) имеет бесконечное множество решений.
2 системы (1) равны нулю, но среди коэффициентов аij(i, j = 1, 2) есть хотя бы один, отличный от нуля, то система (1) имеет бесконечное множество решений.
Легко дать геометрическое истолкование этим предложениям. Поскольку каждому уравнению системы (1) в плоскости соответствует некоторая прямая, то система (1) имеет единственное решение, если прямые имеют одну общую точку; не имеет решений, если прямые параллельны; и имеет бесконечное множество решений, если прямые сливаются.
Правило Крамера решения системы n линейных уравнений с n переменными имеет определенное теоретическое значение; практически им уже при n = 4 не пользуются. Установлено, что число операций умножения и деления, которые необходимо выполнить при решении линейной системы алгебраических уравнений порядка n по формулам Крамера, равно:
N(n) = (n2 — 1)n! + n,
а по схеме единственного деления метода Гаусса:
N(n) = 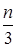 (n2 + 3n — 1).
(n2 + 3n — 1).
Для сравнения объема вычислительной работы по этим двум алгоритмам подсчитаем количество операций:
по Крамеру по Гауссу
при n = 5 2885 65
при n =10 360*106 430
Поэтому все современные ЭВМ имеют стандартные подпрограммы, реализующие различные модификации метода Гаусса.