Формула прямоугольников

Для вычисления приближенного значения интеграла отрезок [a; b] делят на n равных частей точками а = х₀ < x₁ < x₂ <... < x_n = b так, что Тогда длина каждого частичного отрезка 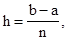а точки разбиения х₀ = а; x₁ = a + h; x₂ = a + 2h;...; x_n-1 = a + (n-1)h; x _n = a + nh = b образуют арифметическую прогрессию с разностью h. Эти точки называют узлами, а h - шагом интегрирования. Затем в узлах вычисляют ординаты y₀, y₁, y₂,..., y_n то есть y_i = f(x_i) для х_i = a + ih (i=0, 1, 2,..., n). На частичных отрезках [x_i, x_i+1] строят прямоугольники (рисунок 5 – 6), высота которых равна значению f(x) в какой-либо точке каждого частичного отрезка.

Тогда произведение f(x_i) * h дает площадь частичного прямоугольника, а сумма таких произведений дает площадь ступенчатой фигуры, представляющую собой приближенное значение интеграла.

Рис. 1.

Если f(x_i) вычисляют (рис.1) в левых концах отрезков [x_i, x_i+1], то получают формулу левых прямоугольников вида:

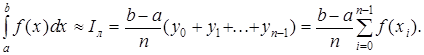
Если f(x_i) вычисляют (рис.6) в правых концах отрезков [x_i, x_i+1], то получают формулу правых прямоугольников вида:

Если же функцию f вычисляют в точках x_i + [x_i, x_i+1], то получают формулу средних прямоугольников вида:

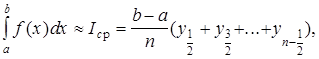(1)

где

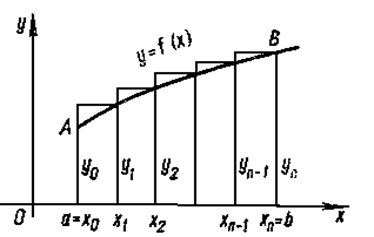
Рис. 2.

В том частном случае, когда функция f монотонно возрастает на [a; b] (рис.2), величина Iл дает значение интеграла I с недостатком (ломанная вписана в криволинейную трапецию), а величина Iп - с избытком (ломаная описана). Их среднее арифметическое значение дает более точный результат: