Краткое теоретическое введение. 1. Методы Эйлера численного решения дифференциальных уравнений первого и второго порядков.

1. Методы Эйлера численного решения дифференциальных уравнений первого и второго порядков.

Метод численного решения дифференциального уравнения первого порядка

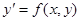(1)

с начальным условием 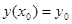основан на разложении решения в ряд Тейлора в 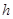-окрестности точки :

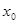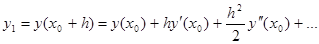
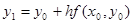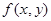При отбрасывании всех членов ряда, содержащих производные второго и высших порядков получим: , где -правая часть уравнения (1).

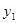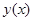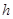Пользуясь значением из разложения в - окрестности точки 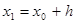получим

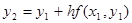(2)

Аналогично продолжая для следующей точки 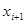, получим

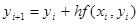(3)

Если дано уравнение второго порядка

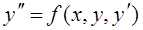(4)

с начальными условиями 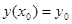и , то как такое уравне- ние можно свести к системе двух уравнений первого порядка

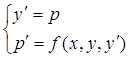, (5)

причем 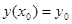и .

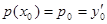Тогда приближенные значения функци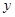й и 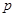в точке 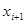можно высислить по формулам

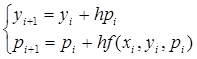, (6)

где 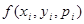- правая часть уравнения (4).

При достаточно малой величине шага 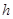метод Эйлера дает решение с большой точностью, т.к. погрешность решения близка к .

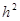2. Методы Рунге-Кутта численного решения дифференциальных уравнений первого и второго порядков.

Пусть дано дифференциальное уравнение первого порядка 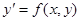с начальным условием .

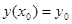Последовательные значения 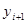искомой функции 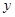определяются по формуле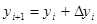

где ,

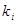- коэффициенты, которые вычисляются по формулам

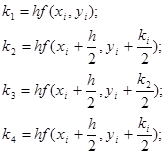
где 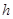- шаг интегрирования;

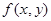- правая часть дифференциального уравнения, разрешенного относительно производной.

Если дано уравнение второго порядка 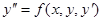с начальными условиями 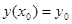и , то как такое уравне- ние можно свести к системе двух уравнений первого порядка

,

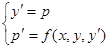причем 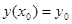и .

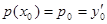Тогда приближенные значения функци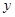й и 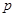можно вычис- лить по формулам

,

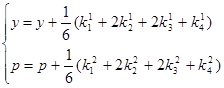где 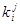- коэффициенты вычисляемые по формулам

,

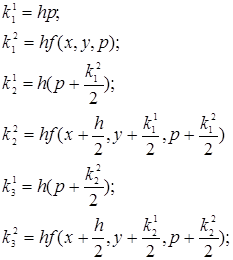
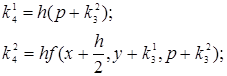где 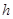- шаг интегрирования;

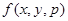- правая часть дифференциального уравнения, разрешенного относительно производной.

Метод Рунге-Кутта применим также для приближенного решения систем обыкновенных дифференциальных уравнений, применяя формулы для каждого уравнения в отдельности. При этом погрешность интегрирования - есть величина порядка .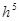

Задание на работу.

1.По указанию преподавателя или в соответствии с вариантом из Таблиц 5 и 6 заданий (см. Приложение) взять условия – дифференциальные уравнения первого и второго порядка, начальные условия, границы отрезка интегрирования и шаг интегрирования.

2.Изучить методы численного решения дифференциальных уравнений первого и высших порядков.

3.На основании формул методов Эйлера и Рунге-Кутта, составить блок-схему и программу для решения дифференциального уравнения первого порядка. Сравнить результаты. Затем шаг принять, равный 0.1× h и повторить расчеты. Сделать выводы.

4.Представить дифференциальное уравнение II порядка в виде системы дифференциальных уравнений I порядка.

5.Составить блок-схему алгоритма и программу решения систем дифференциальных уравнений первого порядка методами Эйлера и Рунге - Кутта. Предусмотреть вывод значения контрольной функции в точках табулирования.

Содержание отчета: титульный лист, тема и цель работы, № варианта задания и собственно задание, описание методов решения дифференциальных уравнений, математическая постановка задачи и определение области допустимых значений (ОДЗ), блок-схема алгоритма, текст программы и результаты её работы. Работу программы студент обязан показать на ПЭВМ.

Контрольные вопросы

1. Обосновать необходимость численного решения дифференциальных уравнений.

2. В каком виде получается решение дифференциального уравнения при решении численными методами?

3. Сущность метода Эйлера решения дифференциальных уравнений.

4. Сущность метода Рунге-Кутта решения дифференциальных уравнений.

5. Каким образом решаются дифференциальные уравнения высших порядков методами Эйлера и Рунге-Кутта.

6. В чем заключается необходимость численного решения дифференциальных уравнений?

7. Назовите известные вам методы численного решения дифференциальных уравнений?

8. На чем основан метод Эйлера решения дифференциальных уравнений? Его преимущества и недостатки.

9. На чем основан метод Рунге-Кутта решения дифференциальных уравнений? Его преимущества и недостатки.

10. Что такое операторная функция?

11. Как задается операторная функция на языке Borland Pascal 7.0?