Лабораторная работа № 8.

Тема: “Статистическая обработка результатов эксперимента”.

Цель работы: изучение принципов обработки статистических результатов эксперимента.

Краткое теоретическое введение.

В различных областях науки, при решении задач идентификации, оптимального управления и т.п., а также в процессе выполнения практических измерений зачастую необходимо не только определить погрешность измерения, но и дать оценку погрешности результатов эксперимента.

Например, для игнорирования грубых погрешностей необходима предварительная статистическая обработка результатов измерений, в общем случае рассматриваемых как случайные величины.

Случайным называется событие, которое при осуществлении определенного комплекса условий может либо произойти, либо не произойти.

Т.о. можно считать, что при проведении повторных наблюдений в одинаковых условиях каждая из множества возможных незначительных причин случайных изменений результатов может появиться или не появиться, может принимать любые значения как по величине, так и по знаку.

Для каждого i-го измерения Х_i случайная абсолютная погрешность вычисляется по формуле D = Х - Х_i, где X – истинное значение измеряемой величины.

Теоретически доказано, что если закон распределения случайной величины является нормальным (в большинстве случаев это так) и систематические погрешности полностью исключены, то истинное значение измеряемой величины равно математическому ожиданию результатов измерений. Математическое ожидание случайной величины - это такое ее значение, вокруг которого группируются результаты отдельных измерений или погрешностей. При ограниченном количестве N наблюдений их результаты характеризуют оценками параметров функции распределения случайной величины.

Оценкой математического ожидания M[Х] служит среднее арифметическое:

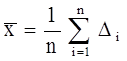
Мерой рассеяния значений случайной величины служит дисперсия D[x], оценка d которой выражается формулой

× .

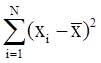Меру рассеяния также характеризуют среднеквадратическим отклонением S[x], оцениваемым величиной, равной G = 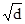. Оценку приписывают каждому из N результатов наблюдений и называют погрешностью единичного измерения, стандартным отклонением или стандартом.

Для проверки вида погрешности и отбрасывания аномальных наблюдений используют критерий

V_i =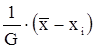

Если, например, для N = 20 выполняется V_i > 2, 71 (c вероятностью 0, 025), то результат i-го измерения считается грубой погрешностью и отбрасывается как аномальный.

Мерой связи между двумя множествами {a} и {b} экспериментальных данных является коэффициент корреляции

r =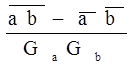

Коэффициент корреляции может принимать значения от -1 до +1. Значение модуля коэффициента корреляции, равное 1, свидетельствует о функциональной зависимости между данными множеств, а нулевое его значение - о полной взаимной независимости элементов множеств.

Задание к работе:

Необходимо произвести статистическую обработку результатов измерений, используя фрагмент протокола поверки прибора (табл.1).

Указания к заполнению табл.1 и обработке результатов:

1. В графу 2 табл. 1 занести последовательность отметок шкалы прибора со следующими пределами измерения и ценой деления:

- для 1, 5, 9, 13 и т.д. вариантов - 60...250 и ценой деления 10;

- для 2, 6, 10, 14 и т.д. вариантов – 0...950 с ценой деления 50;

- для 3, 7, 11, 15 и т.д. вариантов - 30...600 и ценой деления 30;

- для 1, 5, 9, 13 и т.д. вариантов - 0...9.5 и ценой деления 0.5.

Графы 3 и 4 табл.1 заполнить результатами 20 экспериментов, используя функцию - датчик случайных чисел random. При этом использовать следующую формулу

Х = Хшк – h/2 + rnd(h),

где Х – действительное значение при прямом или обратном ходе;

Хшк – поверяемое значение;

rnd(h) – случайная величина в диапазоне 0...h.

Полученную табл.1 распечатать.

Таблица 1

2.Рассчитать математическое ожидание по данным граф 3 и 4.

3.Рассчитать дисперсии и среднеквадратические отклонения по данным 3 и 4 столбцов.

4.Рассчитать критерии {V_i} по данным граф 3 и 4 для каждого эксперимента.

5.Если V_i > 2, 71 (i = 1, 2,..., 20), то i-ый эксперимент считать грубой ошибкой и выдать соответствующее сообщение на экране дисплея.

6.Рассчитать коэффициент корреляции между данными граф 2 и 3 (для четных вариантов) и граф 2 и 4 (для нечетных вариантов), граф 3 и 4 (для всех вариантов). Вывод (распечатка) результатов расчетов должна выводиться на экран дисплея и (или) принтер по запросу программы.

Содержание отчета: титульный лист, тема и цель работы, № варианта задания и собственно задание, математическая постановка задачи и определение области допустимых значений (ОДЗ), блок-схема алгоритма, текст программы, результаты работы программы, выводы.

Контрольные вопросы

1. При решении каких задач в инженерной деятельности возникает необходимость статистической обработки информации?

2. Дайте определения статистических характеристик случайных величин.

3. Что такое прямой и обратный ход?

4. Что такое коэффициент корреляции? Какие значения он может принимать?

5. Типы цикловых структур в Borland Pascal.