Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткое теоретическое введение. Пусть на интервале [a,b] заданы n+1 опорных (узловых) точек a £ xo< x1 < x2 << xn £ b
|
|
Пусть на интервале [a, b] заданы n+1 опорных (узловых) точек a £ xo< x1 < x2 <...< xn £ b. Пусть, кроме того, заданы n+1 действительных чисел yi(i=0, 1, 2,..., n) (например, как значения функции в узловых точках). Под задачей интерполяции понимают нахождение многочлена In(x) степени не больше n такой, что In(xi)=yi для 0 £ i £ n.
Интерполяцию обычно применяют тогда, когда относительно f известны только дискретные значения функции y=f(x), и, чтобы вычислить другие ее значения между узловыми точками (интерполяция) или за отрезком узловых точек (экстраполяция), ее приближают многочленом In(x), причем f(xi)=In(xi) (i=0, 1, 2,..., n).
Всегда существует только один интерполяционный многочлен, который может быть представлен в различной форме.
Форма Лагранжа: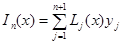 
, где Lj(x) - полиномы n-ой степени, называемые лагранжевыми коэффициентами и имеющие вид:
.
Степень каждого полинома Lj равна n, сам он равен 1 в точке х = xj и обращается в нуль в остальных узлах интерполяции. Формула позволяет вычислять значения полинома Лагранжа и без нахождения его коэффициентов.
У интерполяционного многочлена Лагранжа наблюдается явная зависимость от каждого значения функции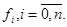 
Это в многих случаях бывает полезно, но при изменении 
интерполяционный многочлен Лагранжа надо строить заново. В этом его недостаток.
Для удобства вычислений целесообразно составить вспомогательную таблицу где хо, x1, …, xn — узлы интерполяции, а х — значение аргумент, для которого определяется приближенное значение по интерполяционной формуле Лагранжа.
,
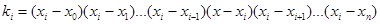Тогда интерполяционный многочлен Лагранжа можно переписать в виде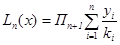 
.
Таблица 1
| 
| 
| … | 
| 
|
| 
| 
| … | 
| 
|
| 
| 
| … | 
| 
|
| … | … | … | … | … | … |
| 
| 
| … |
| 
|
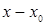
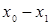
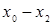
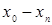
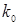
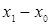
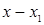
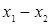
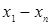
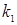
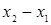
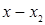
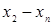
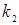
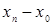
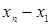
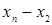
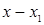
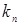
Форма Ньютона: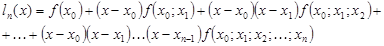 
,
где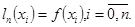 
Интерполяционный многочлен Ньютона содержит не значение функции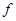 
, а ее разделенные разности. При изменении степени 
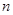у интерполяционного многочлена Ньютона надо добавить или отвергнуть соответствующее количество стандартных слагаемых. Это удобно на практике.
Пусть теперь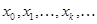 
-произвольные точки (узлы) оси 
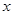, причем 
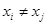при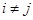 
.
Значение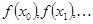 
функции 
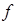в узлах называются разделенными разностями нулевого порядка.
Число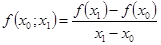 
называется разделенной разностью первого порядка функции 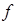(соответственно точкам 
).
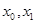Очевидно, что, разделенная разность первого порядка является симметричной функцией аргументов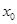 
и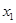 
. 
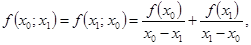
Разделенная разность 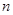-го порядка определяется через разделенные разности 
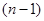-го порядка по рекуррентной формуле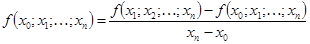 
При вычислениях разделенные разности записывают в виде таблицы.
Таблица 2.
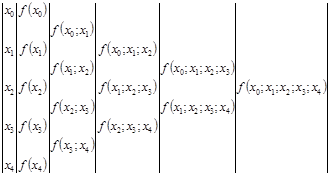
Разделенная разность 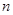-го порядка может быть представлена через узловые значения функции формулой 
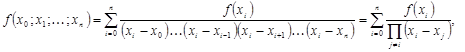то есть симметричной функцией своих аргументов.
Значение разделенной разности не зависит от порядка нумерации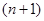 
узлов, по которыми она строится. Всего имеем 
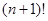вариантов нумерации узлов целыми числами от 0 к .
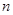Часто применяют равноотстоящие узловые точки (узловые точки, расположенные на равном расстоянии друг от друга):
x0=a; x1=a+h; x2=a+2× h; x3=a+3× h;...; xn =a+n× h=b, т.е. h=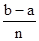 
.
В этом случае разделенные разности выражаются через простые разности:
[xkxk+1xi-2...xk+m]=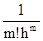 
Dmfk,
где D0fk=fk, D1fk=fk+1-fk, Dmfk=D(Dm-1fk) (m=2, 3,..., k).
Разностная схема упрощается. Формула Ньютона принимает вид
ln(x)=f0+Df0(x-x0)+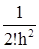 
D2f0(x-x0)(x-x1)+ 
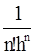Dnf0(x-x0)(x-x1)...(x-xn-1).
Задание к работе
1. В соответствии с вариантом (см. Приложение) или по указанию преподавателя выбрать функцию, интервал (хнач ¸ хкон) и шаг изменения аргумента h.
2. Заполнить массив {Y} значениями функции при каждом значении аргумента x, при этом узлами интерполяции будут значения аргумента от начального до конечного.
3. В соответствии с методами Лагранжа и Ньютона, определить вид интерполяционного многочлена n-ной степени (значение n запросить, по умолчанию n=4). Результаты обоих методов должны совпасть.
4. Используя результаты, полученные в п.3, запросить несколько значений аргумента и выдать соответствующие каждому значению аргумента значение заданной функции и значение интерполяционного многочлена. Вычислить и вывести красным цветом значение абсолютной погрешности для каждого значения х. Если функция в заданной точке не определена, необходимо вывести соответствующее сообщение (красным цветом).
5. Программу составить в соответствии с методологией структурного программирования, выделить подпрограммы и оформить их в виде модуля.
Содержание отчета: титульный лист, тема и цель работы, № варианта задания и собственно задание, описание типов функциональных рядов по методам вычислений, определение типа заданного ряда, математическая постановка задачи и определение области допустимых значений (ОДЗ), блок-схема алгоритма, текст программы и результаты её работы. Работу программы студент обязан показать на ПЭВМ.
Контрольные вопросы
1. Что такое интерполяция?
2. Сущность методов интерполяции по формулам Лагранжа и Ньютона.
3. Для чего используется сплайн-интерполяция?
4. Назначение модулей Borland Pascal. Структура модуля.
5. Основные подпрограммы модуля CRT для работы с цветом.