Формула Симпсона

Для построения формулы Симпсона предварительно рассмотрим такую задачу: вычислить площадь S криволинейной трапеции, ограниченной сверху графиком параболы y = Ax² + Bx + C, слева прямой х = - h, справа прямой x = h и снизу отрезком [-h; h]. Пусть парабола проходит через три точки (рис.8): D(-h; y₀) E(0; y₁) и F(h; y₂), причем х₂ - х₁ = х₁ - х₀ = h. Следовательно,

x₁ = x₀ + h = 0; x₂ = x₀ + 2h.

Тогда площадь S равна интегралу:

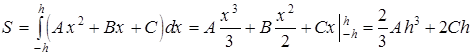. (3)

Выразим эту площадь через h, y₀, y₁ и y₂. Для этого вычислим коэффициенты параболы А, В, С. Из условия, что парабола проходит через точки D, E и F, имеем:

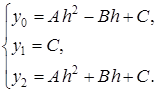
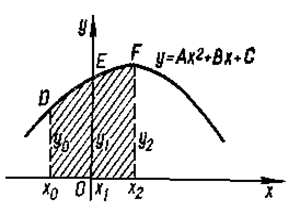
Рис. 4.

Решая эту систему, получаем: C = y₁; A =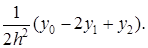

Подставляя эти значения А и С в (3), получаем искомую площадь

(4)

Перейдем теперь к выводу формулы Симпсона для вычисления интеграла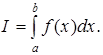

Для этого отрезок интегрирования [a; b] разобьем на 2n равных частей длиной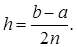

В точках деления (рис.4).а = х₀, х₁, х₂,..., х_2n-2, x_2n-1, x_2n = b,

Вчисляем значения подынтегральной функции f: y₀, y₁, y₂,..., y_2n-2, y_2n-1, y_2n, де y_i = f(x_i), x_i = a + ih (i = 0, 1, 2,..., 2n).

На отрезке [x₀; x₂] подынтегральную функцию заменяем параболой, проходящей через точки (x₀; y₀), (x₁; y₁) и (x₂; y₂), и для вычисления приближенного значения интеграла от х₀ до х₂ воспользуемся формулой (4). Тогда (на рис. 4 заштрихованная площадь):

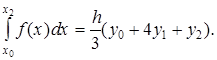
Аналогично находим:

................................................

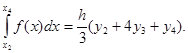
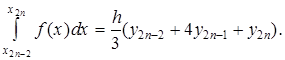
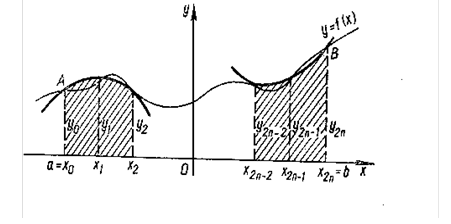
Рис. 5.

Сложив полученные равенства, имеем:

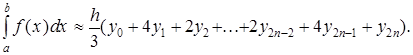
Или 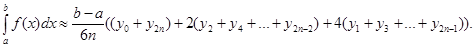(5)

Формула (5) называется обобщенной формулой Симпсона или формулой парабол, так как при ее выводе график подынтегральной функции на частичном отрезке длины 2h заменяется дугой параболы.

Задание на работу:

1. По указанию преподавателя или в соответствии с вариантом из Таблицы 4 заданий (см. Приложение) взять условия – подынтегральную функцию, пределы интегрирования.

2. Составить блок-схему программы и программу, которая должна:

- запросить точность вычисления определенного интеграла, нижний и верхний пределы интегрирования;

- вычислить заданный интеграл методами: для вариантов 1, 4, 7, 10… - правых, для вариантов 2, 5, 8, … - средних; для вариантов 2, 5, 8, … - левых прямоугольников. Вывести количество разбиений диапазона интегрирования, при котором достигнута заданная точность вычисления;

- вычислить заданный интеграл методом трапеций (для четных вариантов) и методом Симпсона (для нечетных вариантов).

- вывести количество разбиений диапазона интегрирования, при котором достигнута заданная точность вычисления;

- вывести значения контрольной функции для заданного значения аргумента и сравнить с вычисленными значениями интеграла. Сделать выводы.

Содержание отчета: титульный лист, тема и цель работы, № варианта задания и собственно задание, описание методов численного интегрирования, математическая постановка задачи, блок-схема алгоритма, текст программы и результаты её работы. Работу программы студент обязан показать на ПЭВМ. Сделать выводы.

Контрольные вопросы

1. Что такое определенный интеграл?

2. Почему наряду с аналитическими методами используются численные методы вычисления определенных интегралов.

3. В чем заключается сущность основных численных методов вычисления определенных интегралов.

4. Влияние количества разбиений на точность вычисления определенного интеграла численными методами.

5. Как вычислить интеграл любым методом с заданной точностью?