Пример выполнения работы № 1

1) A= 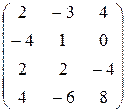; 2) B= 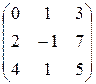3)

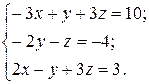
4) , .

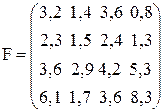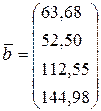Загрузим пакет расширения linalg:

> with(linalg):

1. Введем матрицу 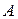, применив функцию matrix и указав в качестве её параметров количество строк и столбцов матрицы, а также список элементов матрицы по строкам:

> A: =matrix(4, 3, [2, -3, 4, -4, 1, 0, 2, 2, -4, 4, -6, 8]);

A: =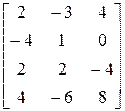

Найдем ранг матрицы 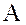с помощью функции rank:

> rank(A);

2

2. Введем матрицу :

> B: =matrix(3, 3, [0, 1, 3, 2, -1, 7, 4, 1, 5]);

B: =

Вычислим определитель матрицы , используя функцию det:

> det(B);

36

Для нахождения матрицы, обратной матрице 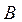, воспользуемся функцией inverse:

> B1: =inverse(B);

B1: =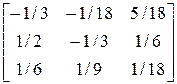

Проверим результат нахождения обратной матрицы. Умножим B на B1, применив функцию multiply:

> E1: = multiply(B, B1);

E1: =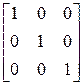

3. Запишем систему, обозначив её идентификатором eqs1. Решим её, используя функцию solve. Параметрами функции будет система eqs1 и её неизвестные:

> eqs1: ={-3*x+y+3*z=10, -2*y-z=-4, 2*x-y+3*z=3};

eqs1: = {-3 x + y + 3 z = 10, -2 y - z = -4, 2 x - y + 3 z = 3}

> a1: =solve(eqs1, {x, y, z});

a1: = {y = 1, x = -1, z = 2}

Эту же систему решим матричным способом и сравним результаты. Решение задается формулой 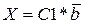, где C1 –матрица, обратная матрице системы уравнений C, – вектор свободных членов.

Введем матрицу системы уравнений C и вектор свободных членов :

> C: =matrix(3, 3, [-3, 1, 3, 0, -2, -1, 2, -1, 3]);

C: =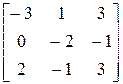

> b: =matrix(3, 1, [10, -4, 3]);

b: =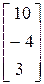

Найдем матрицу 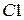, обратную матрицу к C:

> C1: =inverse(C);

C1: =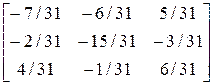

Решением данной системы уравнений будет вектор :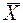

> X: =multiply(C1, b);

X: =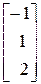

4. Обозначим через 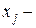объем выпущенной j- ой продукции, 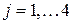. Неизвестные 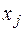найдём из системы

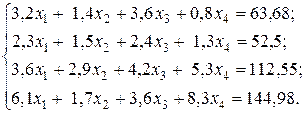
Введём матрицу системы 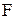, вектор свободных членов 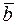и вектор неизвестных .

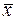> F: =matrix(4, 4, [3.2, 1.4, 3.6, 0.8, 2.3, 1.5, 2.4, 1.3, 3.6, 2.9, 4.2, 5.3, 6.1, 1.7, 3.6, 8.3]);

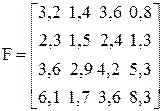
> b: =vector([63.68, 52.5, 112, 55, 144.98]); x: =vector([x1, x2, x3, x4]);

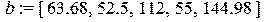
Запишем исходную систему уравнений с помощью функции geneqns и обозначим её идентификатором .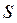

> s: =geneqns(F, x, b);

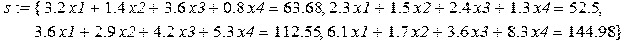
Решим систему 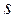с помощью функции solve.

> solve(s, {x1, x2, x3, x4});

{ x3=6.800000000, x1=8.100000000, x2=5.200000000, x4=7.500000000}

Ответ: Объем выпуска продукции составит: x1=8.1, x2=5.2, x3=6.8, x4=7.5.

Контрольные вопросы

1.Что называется матрицей размера ?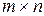

2. Какая матрица называется квадратной, нулевой, единичной?

3. Какие операции можно выполнять с матрицами? Свойства матричных операций.

4. Что понимают под элементарными преобразованиями матрицы?

5. Что называется определителем 2-го, 3-го порядков? Сформулируйте свойства определителей.

6. Что такое миноры матрицы? Что называется алгебраическим дополнением элементов квадратной матрицы?

7. Какая матрица называется невырожденной?

8. Дайте определение обратной матрицы. Всякая ли матрица имеет обратную?

9. Какие методы нахождения обратной матрицы Вы знаете?

10. Что называется рангом матрицы?

11. Какие методы вычисления ранга матрицы Вы знаете?

12. Что называется системой линейных алгебраических уравнений (СЛАУ)?

13. Что называется решением СЛАУ?

14. Какая СЛАУ называется совместной, несовместной? Сформулируйте теорему Кронекера-Капелли.

15. Какие методы решения СЛАУ Вы знаете? В чем они заключаются?

16. Сформулируйте теорему о числе решений СЛАУ.

17. Объясните, как составляется система уравнений в задании 4.